Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 3)
-
402 lượt thi
-
6 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Thực hiện phép tính:
a) (15,25 + 3,75).4 + (20,71 + 5,29).5;
b) 420+1642+615+−35+221+−1021+320;
c) 511.57+511.27+611;
d) (−524+0,75+712):(−218).
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
a) (15,25 + 3,75).4 + (20,71 + 5,29).5
= 19.4 + 26.5
= 76 + 130
= 206
b) 420+1642+615+−35+221+−1021+320
=15+821+25+−35+221+−1021+320
=15+25+−35+821+221+−1021+320
=(15+25+−35)+(821+221+−1021)+320
=1+2+(−3)5+8+2+(−10)21+320
=05+021+320
=0+0+320
=320
c) 511.57+511.27+611
=(511.57+511.27)+611
=511.(57+27)+611
=511.77+611
=511.1+611
=511+611
=5+611
=1111
= 1.
d) (−524+0,75+712):(−218)
=(−524+34+712):(−178)
=(−524+1824+1424):(−178)
=−5+18+1424:(−178)
=98.(−817)
=9.(−8)8.17
=−917
Câu 2:
Tìm x:
a) 23+13⋅x=56;
b) 53,2 : (x – 3,5) + 45,8 = 99
c) (412−2x).1461=612;
d) 12⋅x+150%⋅x=2022
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
a) 23+13⋅x=56
13⋅x=56−23
13⋅x=56−46
13⋅x=16
x=16:13
x=16⋅31
x=12.
Vậy x=12.
b) 53,2 : (x – 3,5) + 45,8 = 99
53,2 : (x – 3,5) = 99 – 45,8
53,2 : (x – 3,5) = 53,2
x – 3,5 = 53,2 : 53,2
x – 3,5 = 1
x = 1 + 3,5
x = 4,5.
Vậy x = 4,5.
c) (412−2x).1461=612.
(92−2x).6561=132
92−2x=132:6561
92−2x=132.6165
92−2x=132.615.13
92−2x=6110
2x=92−6110
2x=4510−6110
2x=−1610
2x=−85
x=−85:2
x=−85.12
x=−45
Vậy x=−45.
d) 12⋅x+150%⋅x=2022
12⋅x+150100⋅x=2022
12⋅x+32⋅x=2022
x.(12+32)=2022
x.42=2022
x . 2 = 2022
x = 2022 : 2
x = 1011
Vậy x = 1011.
Câu 3:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Diện tích trồng cây ăn trái của mảnh vườn là: 23.870=580(m2).
Diện tích trồng rau của mảnh vườn là: 25% . 870 = 217,5 (m2).
Diện tích trồng hoa của mảnh vườn là: 870 – (580 + 217,5) = 72,5 (m2).
Vậy diện tích trồng hoa của mảnh vườn là 72,5 m2.
Câu 4:
Biểu đồ tranh sau đây biểu diễn số lượng buổi học bạn An sử dụng các phương tiện khác nhau để đi đến trường trong tháng 3.

(Mỗi ü ứng với 3 buổi học)
a) Có bao nhiêu buổi học bạn An đi xe máy cùng bố mẹ?
b) Lập bảng thống kê biểu diễn số lượng buổi học bạn An sử dụng các phương tiện đến trường?
c) Tính xác suất bạn An đến trường bằng xe bus (Làm tròn kết quả đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Quan sát biểu đồ tranh ta thấy có bốn hình ü bạn An đi xe máy cùng bố mẹ.
Mà mỗi ü ứng với 3 buổi học.
Số buổi học An đến trường bằng xe máy cùng bố mẹ là: 4.3 = 12 (buổi học).
b) Số buổi học bạn An đi xe bus đến trường là: 3.3 = 9 (buổi học).
Số buổi học bạn An đi phương tiện khác đến trường là: 2.3 = 6 (buổi học).
Ta có bảng thống kê sau:
|
Phương tiện |
Xe bus |
Xe máy (bố mẹ chở) |
Phương tiện khác |
|
Số lượng học sinh |
9 |
12 |
6 |
c) Tổng số buổi học bạn An đi các phương tiện đến trường trong tháng 3 là:
9 + 12 + 6 = 27 (buổi học)
Xác suất bạn An đến trường bằng xe bus là: 927.100%=33,33333.. %
Làm tròn đến chữ số thập phân thứ nhất ta được kết quả là 33,3%.
Câu 5:
a) Quan sát hình vẽ rồi điền vào bảng sau các góc có trong hình vẽ
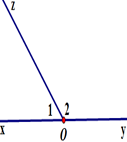
|
Tên góc (cách viết thông thường) |
Kí hiệu |
Tên đỉnh |
Tên cạnh |
|
GócxOz, góc zOx, góc O1 |
^xOz,^zOx,^O1 |
O |
Ox, Oz |
|
|
|
|
|
|
|
|
|
|
b) Cho đoạn thẳng CD = 8 cm. I là điểm nằm giữa C, D. Gọi M, N lần lượt là trung điểm các đoạn thẳng IC, ID. Tính độ dài đoạn thẳng MN.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
|
Tên góc (cách viết thông thường) |
Kí hiệu |
Tên đỉnh |
Tên cạnh |
|
Góc xOz, góc zOx, góc O1 |
^xOz,^zOx,^O1 |
O |
Ox, Oz |
|
Góc yOz, góc zOy, góc O2 |
^yOz,^zOy,^O2 |
O |
Oy, Oz |
|
Góc xOy, góc yOx, góc O |
^xOy,^yOx,ˆO |
O |
Ox, Oy |
b)

Vì điểm M là trung điểm của IC nên ta có: IM=IC2
Điểm Nlà trung điểm của ID nên: IN=ID2
Mặt khác: I nằm giữa C và D nên ta có IC + ID = CD.
Do đó: MN=IM+IN=IC+ID2=CD2=82=4 cm.
Câu 6:
 Xem đáp án
Xem đáp án
Hướng dẫn giải.
M = 1 + 2 + 22 + 23 + 24 + … 22022 + 22023
M = (1 + 2) + (22 + 23) + (24 + 25) + … + (22022 + 22023)
M = (1 + 2) + 22.(1 + 2) + 24.(1 + 2) + … + 22022.(1 + 2)
M = (1 + 2).(1 + 22 + 24 + …+ 22022)
M = 3.(1 + 22 + 24 + …+ 22022) ⁝ 3
Vậy M chia hết cho 3.
