14 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra 45 phút có đáp án (Đề 3)

Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra 45 phút có đáp án

Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra 45 phút có đáp án (Đề 3)

298 lượt thi
14 câu hỏi
0 phút

Danh sách câu hỏi

Câu 1:

Cho mặt phẳng $(α)$ và đường thẳng $d ⊄ (α)$ . Khẳng định nào sau đây sai?

A. Nếu

d / / (α)

thì trong

(α)

tồn tại đường thẳng a sao cho

a / / d

B. Nếu $d / / (α)$ và đường thẳng $b \subset (α)$ thì $b / / d$ .

C. Nếu $d / / c \subset (α)$ thì $d / / (α)$ .

D. Nếu

d \cap (α) = A

và đường thẳng

d^{'} \subset (α)

thì d và d' hoặc cắt nhau hoặc chéo nhau.

Xem đáp án

Chọn B

Câu 2:

Cho hình chóp S.ABCD. Thiết diện của mặt phẳng

(α)

tùy ý với hình chóp không thể là

A. tam giác.

B. ngũ giác.

C. tứ giác.

D. lục giác.

Xem đáp án

Chọn D

Câu 3:

Cho tứ diện ABCD, gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng $(A C D)$ và $(G A B)$ là

A. AM (M là trung điểm của AB).

B. AN (N là trung điểm của CD)

C. AH (H là hình chiếu của B trên CD).

D. AK (K là hình chiếu của C trên BD).

Xem đáp án

Chọn B

Câu 4:

Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD. Gọi I và J lần lượt là hai điểm trên cạnh BC và BD sao cho IJ không song song với CD. Gọi H, K lần lượt là giao điểm của IJ với CD của MH và AC. Giao tuyến của hai mặt phẳng $(A C D)$ và $(I J M)$ là đường thẳng

A. KI.

B. MH.

C. MI.

D. KJ.

Xem đáp án

Chọn B

Câu 5:

Cho tứ diện ABCD, gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, AD, CD, BC. Mệnh đề nào sau đây sai?

M N / / B D

và

M N = \frac{1}{2} B D

B. $M N / / P Q$ và $M N = P Q$ .

C. MNPQ là hình bình hành.

D. MP và NQ chéo nhau.

Xem đáp án

Chọn D

Câu 6:

Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm IJ lần lượt là trọng tâm tam giác SAB, SAD và M là trung điểm CD. Khẳng định nào sau đây đúng?

A. $I J / / (S B D)$

B. $I J / / (S B M)$

C. $I J / / (S B C)$

D. $I J / / (S C D)$

Xem đáp án

Chọn A

Câu 7:

Cho tứ diện ABCD, gọi M, N lần lượt là trung điểm của AB và AC. Lấy E là điểm trên cạnh CD. Thiết diện tạo bởi mặt phẳng và tứ diện ABCD là

A. tam giác MNE.

B. tứ giác MNEF với F là điểm bất kì trên cạnh BD.

C. hình bình hành MNEF với F là điểm trên cạnh BD mà $E F / / B C$ .

D. hình thang MNEF với F là điểm trên cạnh BD mà

E F / / B C

Xem đáp án

Chọn D

Câu 8:

Cho tứ diện ABCD. Gọi E, F, G là các điểm lần lượt thuộc các cạnh AB, AC, BD sao cho EF cắt BC tại I, EG cắt AD tại H. Ba đường thẳng nào sau đây đồng quy?

A. CD, EF, EG.

B. CD, IG, HF.

C. AB, IG, HF.

D. AC, IG, BD.

Xem đáp án

Chọn B

Câu 9:

Cho tứ diện ABCD, gọi I, J theo thứ tự lần lượt là trung điểm của AC và AD, G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng $(G I J)$ và $(B C D)$ là đường thẳng

A. qua I và song song với AB.

B. qua J và song song với BD.

C. qua G và song song với CD.

D. qua G và song song với BC.

Xem đáp án

Chọn C

Câu 10:

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. M là điểm trên cạnh SA sao cho $\frac{S M}{S A} = \frac{2}{3}$ mặt phẳng $(α)$ đi qua M song song với AB và AD, cắt hình chóp theo một tứ giác có diện tích là

A. $\frac{2 a^{2}}{9}$

B. $\frac{2 a^{2}}{3}$

C. $\frac{4 a^{2}}{9}$

D. $\frac{16 a^{2}}{9}$

Xem đáp án

Chọn C

Câu 11:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm các cạnh AB và SD.

a) Tìm giao tuyến của (SAC) và (SDM).

Xem đáp án

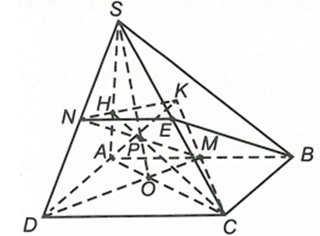
a) Gọi $A C \cap D M = \{O\}$

Ta có $\{\begin{cases} O \in A C \subset (S A C) \\ O \in D M \subset (S D M) \end{cases} \Rightarrow$ O là điểm chung của $(S A C)$ và $(S D M)$ .

Ta có $S \in (S A C)$ , $S \in (S D M) \Rightarrow$ S là điểm chung của $(S A C)$ và $(S D M)$ .

Do vậy

(S A C) \cap (S D M) = S O

Câu 12:

b) Tìm giao điểm H của đường thẳng SA và (MNC)

Xem đáp án

b) Gọi $S O \cap M N = \{P\}$

Do đó $(S A C) \cap (M N C) = C P$

Gọi $S A \cap C P = \{H\}$

Ta có

\{\begin{cases} S A \subset (S A C) \\ (S A C) \cap (M N C) = C P \\ S A \cap C P = \{H\} \end{cases} \Rightarrow S A \cap (M N C) = \{H\}

Câu 13:

c) Chứng minh các đường thẳng CM, AD, HN đồng quy.

Xem đáp án

c) Gọi $C M \cap D A = \{K\}$

Ta có $\{\begin{cases} K \in C M \subset (C M N) \\ K \in D A \subset (S A D) \end{cases} \Rightarrow$ K là điểm chung của $(C M N)$ và (SAD)

Ta có $\{\begin{cases} N \in (C M N) \\ N \in S D \subset (S A D) \end{cases} \Rightarrow$ N là điểm chung của (CMN) và (SAD)

Do đó $(C M N) \cap (S A D) = N K$ (1)

Ta có $\{\begin{cases} H \in C P \subset (C M N) \\ H \in S A \subset (S A D) \end{cases} \Rightarrow$ H là điểm chung của hai mặt phẳng (CMN) và (SAD).

Do đó $(C M N) \cap (S A D) = N H$ (2)

Từ và suy ra ba điểm N, H, K cùng thuộc giao tuyến của (CMN) và (SAD) nên N, H, K thẳng hàng hay K thuộc đường thẳng NH.

Vậy các đường thẳng CM, AD, HN đồng quy tại K

Câu 14:

d) Chứng minh đường thẳng MN song song với (SBC)

Xem đáp án

d) Ta có N là điểm chung của (BMN) và (SCD).

Mà $B M / / C D \Rightarrow (B M N) \cap (S C D) = N E$ , với E là giao điểm đường thẳng qua N và song song AB.

Do đó $N E / / M B$ , $N E = M B$ (cùng song song và bằng nửa AB) nên MNEB là hình bình hành $\Rightarrow M N / / E B$

Mặt khác

E B \subset (S B C) \Rightarrow M N / / (S B C)

Bắt đầu thi ngay

Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra 45 phút có đáp án

Đề kiểm tra học kì 2 Chuyên đề toán 11: Kiểm tra 45 phút có đáp án (Đề 3)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương