17 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa kì 1 Toán 8 CD có đáp án (Đề 2)

Câu 1:

Trong các biểu thức sau, biểu thức nào là đơn thức bậc 5?

A. $x^{5} y + 1$

B. $x^{2} + y^{3}$

C. $x^{2} y^{5}$

D. $x y^{2} z x$

Xem đáp án

Đáp án đúng là: D

Ta có: $x y^{2} z x = x^{2} y^{2} z$ là đơn thức bậc 5.

Câu 2:

Đơn thức nào sau đây đồng dạng với đơn thức $- 3 x^{2} y$ ?

A. $\frac{1}{2} x y x$

B. $3 x^{2} y z$

C. $x y^{2}$ $- 3 x^{2} z$

D. $- 3 x^{2} z$

Xem đáp án

Đáp án đúng là: A

Ta có: $\frac{1}{2} x y x = \frac{1}{2} x^{2} y$ , đơn thức này đồng dạng với đơn thức $- 3 x^{2} y$ .

Câu 3:

Giá trị của biểu thức $A = \frac{1}{2} x y^{2} + \frac{2}{3} x^{2} y + x y + x y^{2} - \frac{1}{3} x^{2} y$ tại $x = \frac{1}{2}$ và $y = - 1$ là

A. $\frac{1}{6}$

B. $\frac{4}{3}$

C. $\frac{1}{3}$

D. $\frac{7}{6}$

Xem đáp án

Đáp án đúng là: A

Ta có: $A = (\frac{1}{2} x y^{2} + x y^{2}) + (\frac{2}{3} x^{2} y - \frac{1}{3} x^{2} y) + x y$

$= \frac{3}{2} x y^{2} + \frac{1}{3} x^{2} y + x y$

Thay $x = \frac{1}{2}$ và $y = - 1$ vào biểu thức $A = \frac{3}{2} x y^{2} + \frac{1}{3} x^{2} y + x y$ ta được:

$A = \frac{3}{2} . \frac{1}{2} . {(- 1)}^{2} + \frac{1}{3} . {(\frac{1}{2})}^{2} . (- 1) + \frac{1}{2} . (- 1) = \frac{3}{4} - \frac{1}{12} - \frac{1}{2} = \frac{1}{6}$

.

Câu 4:

Chọn đẳng thức sai trong các đẳng thức sau đây:

A. ${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ ${(- a - b)}^{3} = - a^{3} - 3 a^{2} b - 3 a b^{2} - b^{3}$

B.

C. ${(- a + b)}^{3} = - a^{3} - 3 a^{2} b + 3 a b^{2} + b^{3}$

D. ${(a - b)}^{3} = a^{3} - 3 a^{2} b + 3 a b^{2} - b^{3}$

Xem đáp án

Đáp án đúng là: C

Ta có:

{(- a + b)}^{3} = {(b - a)}^{3} = b^{3} - 3 b^{2} a + 3 b a^{2} - a^{3} = - a^{3} + 3 a^{2} b - 3 a b^{2} + b^{3}

Câu 5:

Phân thức $\frac{1 - x}{y - x}$ bằng với phân thức nào sau đây?

A. $\frac{x - 1}{y - x}$

B. $\frac{1 - x}{x - y}$

C. $\frac{x - 1}{x - y}$

D. $\frac{y - x}{1 - x}$

Xem đáp án

Đáp án đúng là: C

Ta có: . $\frac{1 - x}{y - x} = \frac{- (x - 1)}{- (x - y)} = \frac{x - 1}{x - y}$

Câu 6:

Kết quả của phép tính $\frac{5 x + 7}{3 x y} - \frac{2 x - 5}{3 x y}$ là

A. $\frac{3 x + 2}{3 x y}$

B. $\frac{3 x - 2}{3 x y}$

C. $\frac{x - 4}{x y}$

D. $\frac{x + 4}{x y}$

Xem đáp án

Đáp án đúng là: D

Ta có:

\frac{5 x + 7}{3 x y} - \frac{2 x - 5}{3 x y} = \frac{5 x + 7 - 2 x + 5}{3 x y} = \frac{3 x + 12}{3 x y} = \frac{3 (x + 4)}{3 x y} = \frac{x + 4}{x y}

Câu 7:

Hình nào sau đây là hình chóp tứ giác đều?

A. Hình có đáy là tứ giác;

B. Hình có đáy là hình vuông;

C. Hình có đáy là hình vuông và tất cả các cạnh bên bằng nhau;

D. Hình có đáy là tam giác đều và có một cặp cạnh bên vuông góc với nhau.

Xem đáp án

Đáp án đúng là: C

Hình có đáy là hình vuông và tất cả các cạnh bên bằng nhau là hình chóp tứ giác đều.

Câu 8:

Một hình chóp tam giác đều có chiều cao h, thể tích V. Diện tích đáy S là

A. $S = \frac{h}{V}$

B. $S = \frac{V}{h}$

C. $S = \frac{3 V}{h}$

D. $S = \frac{3 h}{V}$

Xem đáp án

Đáp án đúng là: C

Ta có thể tích của hình chóp tam giác đều là $V = \frac{1}{3} S h$

Suy ra $S = \frac{3 V}{h}$ .

Câu 9:

Thu gọn biểu thức:

a) $\frac{3}{4} x^{3} y^{3} : (- \frac{1}{2} x^{2} y^{2});$

b) $x (x - y) + y (x + y)$ ;

c) $(x + 3 y) (x - 2 y) - (x^{4} y - 6 x^{2} y^{3}) : x^{2} y$ .

Xem đáp án

a) $\frac{3}{4} x^{3} y^{3} : (- \frac{1}{2} x^{2} y^{2})$

$= [\frac{3}{4} : (- \frac{1}{2})] \cdot (x^{3} : x^{2}) \cdot (y^{3} : y^{2})$

$= - \frac{3}{2} x y .$

b) $x (x - y) + y (x + y)$

$= x^{2} - x y + x y + y^{2}$

$= x^{2} + y^{2}$

c) $(x + 3 y) (x - 2 y) - (x^{4} y - 6 x^{2} y^{3}) : x^{2} y$

$= x^{2} - 2 x y + 3 x y - 6 y^{2} - (x^{2} - 6 y^{2})$

$= x^{2} + x y - 6 y^{2} - x^{2} + 6 y^{2}$

$= x y$

Câu 10:

a) $5 x^{2} (x - y) - 15 x y (y - x)$ ; b) $x^{6} - 1$ ; c) $3 x^{2} + 5 x - 3 y^{2} - 5 y$ .

Xem đáp án

a) $5 x^{2} (x - y) - 15 x y (y - x)$

$= 5 x^{2} (x - y) + 15 x y (x - y)$

$= (x - y) (5 x^{2} + 15 x y)$

$= 5 x (x - y) (x + 3 y) .$

b) $x^{6} - 1$

$= {(x^{3})}^{2} - 1^{2}$

$= (x^{3} - 1) (x^{3} + 1)$

$= (x - 1) (x^{2} + x + 1) (x + 1) (x^{2} - x + 1) .$

c) $3 x^{2} + 5 x - 3 y^{2} - 5 y$

$= (3 x^{2} - 3 y^{2}) + (5 x - 5 y)$

$= 3 (x^{2} - y^{2}) + 5 (x - y)$

$= 3 (x - y) (x + y) + 5 (x - y)$

$= (x - y) (3 x + 3 y + 5)$

Câu 11:

a) Rút gọn biểu thức A.

Xem đáp án

$A = \frac{x + 15}{x^{2} - 9} + \frac{2}{x + 3}$

a) Với $x \neq \pm 3$ ta có:

$A = \frac{x + 15}{x^{2} - 9} + \frac{2}{x + 3} = \frac{x + 15}{(x + 3) (x - 3)} + \frac{2}{x + 3}$

$= \frac{x + 15 + 2 (x - 3)}{(x + 3) (x - 3)}$ $= \frac{x + 15 + 2 x - 6}{(x + 3) (x - 3)}$

$= \frac{3 x + 9}{(x + 3) (x - 3)}$ $= \frac{3 (x + 3)}{(x + 3) (x - 3)} = \frac{3}{x - 3}$

Vậy với $x \neq \pm 3$ thì $A = \frac{3}{x - 3} .$

Câu 12:

b) Tìm x để A có giá trị bằng $\frac{- 1}{2}$ .

Xem đáp án

b) Với $x \neq \pm 3$ , để $A = \frac{- 1}{2}$ thì ta có: $\frac{3}{x - 3} = \frac{- 1}{2}$

Suy ra $- x + 3 = 6$

Do đó $x = - 3$ (không thỏa mãn)

Vậy không có giá trị nào của x để $A = \frac{- 1}{2} .$

Câu 13:

c) Tìm số tự nhiên x để A có giá trị nguyên.

Xem đáp án

Với $x \neq \pm 3$ , để A nguyên thì $\frac{3}{x - 3} \in ℤ$ , tức $x - 3 \in$ Ư(3)

Mà Ư $(3) = \{\pm 1; \pm 3\}$ , ta có bảng sau:

x - 3	-3	-1	1	3
x	0	2	4	6

Các giá trị x tìm được ở trên đều thỏa mãn điều kiện $x \neq \pm 3$ và x là số tự nhiên.

Vậy $x \in \{0; 2; 4; 6\}$ .

Câu 14:

Một chiếc lều ở một trại hè của học sinh tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ bên.

a) Thể tích không khí bên trong lều là bao nhiêu (làm tròn kết quả đến chữ số thập phân thứ hai)?

b) Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, ...) là bao nhiêu (làm tròn kết quả đến chữ số thập phân thứ hai)? Biết độ dài trung đoạn của lều trại là 2,24cm.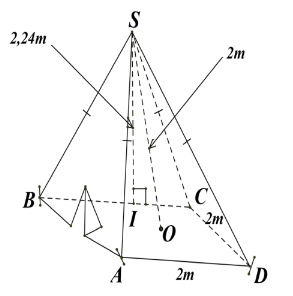

Một chiếc lều ở một trại hè của học sinh tham gia cắm trại có dạng hình chóp tứ giác đều theo các kích thước như hình vẽ bên (ảnh 1)

Xem đáp án

a) Thể tích không khí bên trong lều chính là thể tích hình chóp tứ giác đều:

$V = \frac{1}{3} S h = \frac{1}{3} {.2}^{2} .2 = \frac{8}{3} \approx 2,67$ (m³).

b) Số mét vải bạt cần thiết để dựng lều chính là diện tích xung quanh hình chóp tứ giác đều và bằng:

$S_{x q} = \frac{1}{2} C d = \frac{1}{2} (2.4) .2,24 \approx 8,96$ (m²).

Câu 15:

Cho tứ giác MNPQ có PM là tia phân giác của

\hat{N P Q}

,

\hat{Q M N} = 110 °, \hat{N} = 120 °, \hat{Q} = 60 °

. Tính số đo của

\hat{M P Q}

và

\hat{Q M P} .

Cho tứ giác MNPQ có PM là tia phân giác của góc NPQ,, QMN = 110 độ, góc N = 120 độ, Q = 60 độ . Tính số đo của góc MPQ và góc QMP (ảnh 1)

Xem đáp án

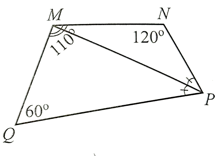
Trong tứ giác MNPQ, ta có: $\hat{Q} + \hat{Q M N} + \hat{N} + \hat{N P Q} = 360 °$

Suy ra $\hat{N P Q} = 360 ° - (\hat{Q M N} + \hat{N} + \hat{Q}) = 360 ° - (110 ° + 120 ° + 60 °) = 70 °$ .

Do PM là tia phân giác của góc NPQ nên ta có:

$\hat{N P M} = \hat{M P Q} = \frac{\hat{N P Q}}{2} = \frac{70 °}{2} = 35 °$ .

Trong tam giác MPQ, ta có: $\hat{Q} + \hat{Q M P} + \hat{M P Q} = 180 °$

Suy ra $\hat{Q M P} = 180 ° - (\hat{M P Q} + \hat{Q}) = 180 ° - (35 ° + 60 °) = 85 °$ .

Vậy $\hat{N P M} = \hat{M P Q} = 35 °$ , $\hat{Q M P} = 85 °$ .

Câu 16:

Tính chiều dài đường trượt AC trong hình vẽ bên (kết quả làm tròn hàng phần mười).

Xem đáp án

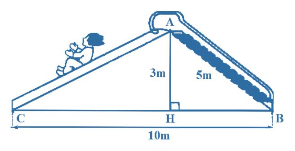
Áp dụng định lí Pythagore trong tam giác AHB vuông tại H ta có:

$A B^{2} = A H^{2} + H B^{2}$

Suy ra $H B^{2} = A B^{2} - A H^{2} = 5^{2} - 3^{2} = 25 - 9 = 16$

Do đó $H B = \sqrt{16} = 4$ cm, nên $C H = B C - H B = 10 - 4 = 6$ cm.

Áp dụng định lí Pythagore trong tam giác AHC vuông tại H ta có:

$A C^{2} = A H^{2} + H C^{2} = 3^{2} + 6^{2} = 9 + 36 = 45$

Suy ra $A C = \sqrt{45} \approx 6,7$ m.

Vậy chiều dài đường trượt AC là $6,7$ m.

Câu 17:

Cho ba số thực a, b, c khác 0 thỏa mãn $a^{3} + b^{3} + c^{3} = 3 a b c .$ Tính giá trị của biểu thức $A = (1 + \frac{a}{b}) (1 + \frac{b}{c}) (1 + \frac{c}{a}) .$

Xem đáp án

Ta có: $a^{3} + b^{3} + c^{3} - 3 a b c$

$= {(a + b)}^{3} - 3 a b (a + b) + c^{3} - 3 a b c$

$= {(a + b)}^{3} + c^{3} - 3 a b (a + b) - 3 a b c$

$= {(a + b)}^{3} + c^{3} - 3 a b (a + b + c)$

$= (a + b + c) [{(a + b)}^{2} - (a + b) c + c^{2}] - 3 a b (a + b + c)$

$= (a + b + c) (a^{2} + b^{2} + c^{2} - a b - b c - c a)$

Suy ra $a^{3} + b^{3} + c^{3} = 3 a b c$ hay $a^{3} + b^{3} + c^{3} - 3 a b c = 0$

Nên $a + b + c = 0$ hoặc $a^{2} + b^{2} + c^{2} - a b - b c - c a = 0 (*)$

Mặt khác $2 (a^{2} + b^{2} + c^{2} - a b - b c - c a) = 2 a^{2} + 2 b^{2} + 2 c^{2} - 2 a b - 2 b c - 2 c a$

$= {(a - b)}^{2} + {(b - c)}^{2} + {(c - a)}^{2}$

Do đó $a^{2} + b^{2} + c^{2} - a b - b c - c a = \frac{1}{2} [{(a - b)}^{2} + {(b - c)}^{2} + {(c - a)}^{2}] \geq 0$ với mọi a, b, c

Nên để (*) xảy ra thì $\{\begin{cases} {(a - b)}^{2} = 0 \\ {(b - c)}^{2} = 0 \\ {(c - a)}^{2} = 0 \end{cases}$ , hay $\{\begin{cases} a - b = 0 \\ b - c = 0 \\ c - a = 0 \end{cases}$ tức $a = b = c$ .

⦁ Trường hợp 1: $a + b + c = 0$

Suy ra $a + b = - c; b + c = - a; c + a = - b$

Khi đó $A = (1 + \frac{a}{b}) (1 + \frac{b}{c}) (1 + \frac{c}{a}) = \frac{a + b}{b} . \frac{b + c}{c} . \frac{c + a}{a} = \frac{- c}{b} . \frac{- a}{c} . \frac{- b}{a} = - 1.$

⦁ Trường hợp 2: $a = b = c$ thì ta được $A = (1 + \frac{a}{b}) (1 + \frac{b}{c}) (1 + \frac{c}{a}) = 2.2.2 = 8$ .

Đề kiểm tra Giữa kì 1 Toán 8 CD có đáp án

Đề kiểm tra Giữa kì 1 Toán 8 CD có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương