Đề kiểm tra Giữa học kì 2 Toán 6 có đáp án (Đề 3)
-
246 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Lời giải:
\(\frac{a}{b}\) là phân số khi a, b \( \in \mathbb{Z}\), b\( \ne \)0.
Câu 2:
Cho biểu đồ tranh

Trong các khẳng định sau đây khẳng định nào sai:
 Xem đáp án
Xem đáp án
Lời giải:
D) sai vì số học sinh đạt điểm 10 trong tuần là 14
Câu 3:
Cho hình vẽ:
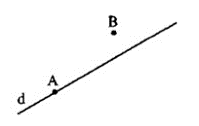
Khẳng định nào sau đây sai:
 Xem đáp án
Xem đáp án
Lời giải:
C) sai vì đường thẳng d chỉ đi qua điểm A mà không đi qua điểm B.
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải:
Vì O nằm giữa M và N nên OM + ON = NM
5 + 3 = 8cm
Vậy MN = 8cm
Câu 5:
 Xem đáp án
Xem đáp án
Lời giải:
Xác suất xuất hiện mặt ngửa khi tung đồng xu là:
22 : 50 = \(\frac{{22}}{{50}} = \frac{{22:2}}{{50:2}} = \frac{{11}}{{25}}\)
Câu 6:
Phân số nghịch đảo của phân số \(\frac{{15}}{7}\) là:
 Xem đáp án
Xem đáp án
Lời giải:
Hai phân số là nghịch đảo của nhau nếu tích của chúng bằng 1.
Ta có: \(\frac{{15}}{7}.\frac{7}{{15}} = \frac{{15.7}}{{7.15}} = 1\)
Câu 7:
II. Tự luận
Thực hiện phép tính
a)
b) \(\frac{5}{9}.\frac{7}{{13}} + \frac{5}{9}.\frac{9}{{13}} + \frac{3}{{13}}.\frac{{ - 5}}{9}\)
c) \(\frac{{ - 3}}{7} + \frac{{ - 22}}{{26}} + \left( {\frac{2}{{ - 13}} + \frac{3}{7} + {{2021}^0}} \right)\)
 Xem đáp án
Xem đáp án
a) \(\left( {\frac{9}{{16}} - \frac{5}{8} + \frac{3}{4}} \right):\frac{{11}}{{32}}\)
\( = \left( {\frac{9}{{16}} - \frac{{10}}{{16}} + \frac{{12}}{{16}}} \right):\frac{{11}}{{32}}\)
\( = \left( {\frac{{9 - 10 + 12}}{{16}}} \right):\frac{{11}}{{32}}\)
\( = \frac{{11}}{{16}}:\frac{{11}}{{32}}\)
\( = \frac{{11}}{{16}}.\frac{{32}}{{11}}\)
\( = \frac{{11.32}}{{16.11}}\)
\( = \frac{{11.16.2}}{{16.11}} = 2\)
b) \(\frac{5}{9}.\frac{7}{{13}} + \frac{5}{9}.\frac{9}{{13}} + \frac{3}{{13}}.\frac{{ - 5}}{9}\)
\( = \frac{5}{9}.\frac{7}{{13}} + \frac{5}{9}.\frac{9}{{13}} - \frac{5}{9}.\frac{3}{{13}}\)
\( = \frac{5}{9}.\left( {\frac{7}{{13}} + \frac{9}{{13}} - \frac{3}{{13}}} \right)\)
\( = \frac{5}{9}.\left( {\frac{{7 + 9 - 3}}{{13}}} \right)\)
\( = \frac{5}{9}.\frac{{13}}{{13}} = \frac{5}{9}.1 = \frac{5}{9}\)
c) \(\frac{{ - 3}}{7} + \frac{{ - 22}}{{26}} + \left( {\frac{2}{{ - 13}} + \frac{3}{7} + {{2021}^0}} \right)\)
\( = \frac{{ - 3}}{7} + \frac{{ - 22}}{{26}} + \left( {\frac{2}{{ - 13}} + \frac{3}{7} + 1} \right)\)
\( = \frac{{ - 3}}{7} + \frac{{ - 22}}{{26}} + \frac{2}{{ - 13}} + \frac{3}{7} + 1\)
\( = \left( {\frac{{ - 3}}{7} + \frac{3}{7}} \right) + \left( {\frac{{ - 22}}{{26}} + \frac{2}{{ - 13}}} \right) + 1\)
\( = \left( {\frac{{ - 3 + 3}}{7}} \right) + \left( {\frac{{ - 22}}{{26}} + \frac{{ - 4}}{{26}}} \right) + 1\)
\( = \frac{0}{7} + \frac{{\left( { - 22} \right) + \left( { - 4} \right)}}{{26}} + 1\)
\( = 0 + \frac{{ - 26}}{{26}} + 1\)
\( = 0 + ( - 1) + 1 = 0\)
Câu 8:
Tìm x
a) \(\frac{7}{8} + x = \frac{3}{5}\)
b)
 Xem đáp án
Xem đáp án
a) \(\frac{7}{8} + x = \frac{3}{5}\)
\(x = \frac{3}{5} - \frac{7}{8}\)
\(x = \frac{{24}}{{40}} - \frac{{35}}{{40}}\)
\(x = \frac{{24 - 35}}{{40}}\)
\(x = \frac{{ - 11}}{{40}}\)
b) \(\frac{2}{3}\left( {2x - 1} \right) = \frac{{ - 4}}{{21}}\)
\[2x - 1 = \frac{{ - 4}}{{21}}:\frac{2}{3}\]
\[2x - 1 = \frac{{ - 4}}{{21}}.\frac{3}{2}\]
\[2x - 1 = \frac{{ - 2}}{7}\]
\[2x = \frac{{ - 2}}{7} + 1\]
\[2x = \frac{5}{7}\]
\[x = \frac{5}{7}:2\]
\[x = \frac{5}{7}.\frac{1}{2}\]
\[x = \frac{5}{{14}}\]
Câu 9:
a) Trong ba điểm O; B; A điểm nào nằm giữa hai điểm còn lại? Vì sao?
b) A có phải trung điểm của OB không? Vì sao?
 Xem đáp án
Xem đáp án
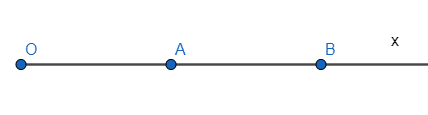
a) Ta có ba điểm A, B, C thuộc tia Ox và OA < OB (3 < 6) nên A nằm giữa O và B.
b) Vì A nằm giữa O và B nên AO + BA = OB
Thay số: 3 + AB = 6
AB = 6 – 3
AB = 3cm
Vì A nằm giữa O và B; OA = AB = \(\frac{{OB}}{2} = \frac{6}{2} = 3cm\) nên A là trung điểm của OB
Câu 10:
Chứng minh rằng
A = \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{10}^2}}} < 1\)
 Xem đáp án
Xem đáp án
Chứng minh rằng
A = \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{10}^2}}} < 1\)
Ta có: \(\frac{1}{{{2^2}}} = \frac{1}{{2.2}} < \frac{1}{{1.2}}\)
\(\frac{1}{{{3^2}}} = \frac{1}{{3.3}} < \frac{1}{{2.3}}\)
\(\frac{1}{{{4^2}}} = \frac{1}{{4.4}} < \frac{1}{{3.4}}\)
…
\(\frac{1}{{{{10}^2}}} = \frac{1}{{10.10}} < \frac{1}{{9.10}}\)
Nên \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{10}^2}}} < \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{9.10}}\)
A <\(\frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{9.10}}\)
Ta lại có: \(\frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{9.10}}\) = 1 - \(\frac{1}{2} + \frac{1}{2} - \frac{1}{3} + ... + \frac{1}{9} - \frac{1}{{10}} = 1 - \frac{1}{{10}} = \frac{9}{{10}}\)
Vì \(\frac{9}{{10}} < 1\) nên A < 1
