Đề kiểm tra Giữa học kì 2 Toán 6 có đáp án (Đề 2)
-
313 lượt thi
-
12 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 2:

Tìm khẳng định sai trong các khẳng định sau:
 Xem đáp án
Xem đáp án
Lời giải:
Nhà Mai trồng 5 cây hoa; nhà Lan trồng 5 cây hoa; nhà Huy trồng 3 cây hoa; nhà An trồng 6 cây hoa.
Khẳng định A đúng vì nhà An trồng nhiều hoa nhất (6 cây).
Khẳng định B đúng vì nhà Huy trồng ít hoa nhất (3 cây) .
Khẳng định C đúng vì nhà Lan và nhà Mai trồng số cây hoa bằng nhau( 5 cây).
Khẳng định D sai vì nhà Lan và nhà Mai trồng được 10 cây hoa còn nhà nhà Huy và An trồng được 9 cây hoa.
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải:
Vì O là trung điểm của AB nên OB = OB = AB2=122 = 6cm
Câu 4:
 Xem đáp án
Xem đáp án
Lời giải:
Hai phân số được gọi là đối nhau nếu tổng của chúng bằng 0.
Ta có: −38+(−(−38))=−38+(−−38)=−38+38=(−3)+38=08=0
Câu 5:
 Xem đáp án
Xem đáp án
Lời giải:
Xác suất thực nghiệm xuất hiện mặt 5 chấm là:
4 : 10 = 410
Câu 7:
 Xem đáp án
Xem đáp án
Lời giải:
A) sai vì cần thêm điều kiện hai tia đó phải nằm về hai phía của gốc
B) sai vì cần thêm điều kiện hai tia đó phải nằm về một phía của gốc
C) đúng vì nó là định nghĩa về tia
D) sai vì tia bị giới hạn 1 đầu là gốc của tia
Câu 8:
 Xem đáp án
Xem đáp án
Lời giải:
Ta có: 27=2.87.8=1656
5−8=5.(−7)(−8).(−7)=−3556
Câu 9:
II. Tự luận
Thực hiện phép tính:
a) 2−9−5−36−14
b) (−4−14−3−15)−(15−2035−−17)
c) 37.911+37.511−37.2511
 Xem đáp án
Xem đáp án
a) 2−9−5−36−14
=2.4(−9).4−5−36−1.(−9)4.(−9)
=8−36−5−36−−9−36
=8−5−(−9)−36
=12−36=12:(−12)(−36):(−12)
=−13
b) (−4−14−3−15)−(15−2035−−17)
=−4−14−3−15−15+2035+−17
=(−4−14+−17)+(−3−15−15+2035)
=((−4):(−2)(−14):(−2)+−17)+(3:315:3−15+20:535:5)
=(27+−17)+(15−15+47)
=17+47=57
c) 37.911+37.511−37.2511
=37.(911+511−2511)
=37.(9+5−2511)
=37.−1111=37.(−1)=−37
Câu 10:
Xếp loại thi đua ba tổ lao động của một đội sản xuất được thống kê như sau (đơn vị: người):
|
Tổ |
Giỏi |
Khá |
Đạt |
|
Tổ 1 |
8 |
3 |
1 |
|
Tổ 2 |
9 |
2 |
1 |
|
Tổ 3 |
7 |
4 |
1 |
a) Mỗi tổ lao động có bao nhiêu người.
b) Đội trưởng thông báo rằng số lao động giỏi của cả đội nhiều hơn số lao động khá và đạt của cả đội là 12 người. Đội trưởng thông báo đúng hay sai.
 Xem đáp án
Xem đáp án
a) Số người lao động của tổ 1 là:
8 + 3 + 1 = 12 (người)
Số người lao động của tổ 2 là:
9 + 2 + 1 = 12 (người)
Số người lao động của tổ ba là:
7 + 4 + 1 = 12 (người)
b) Số lao động giỏi của cả đội là:
8 + 9 + 7 = 24 (người)
Số lao động khá của cả đội là:
3 + 2 + 4 = 9 (người)
Số lao động đạt của cả đội là:
1 + 1 + 1 = 3 (người)
Số lao động giỏi nhiều hơn số lao động khá và đạt của đội số người là:
24 – (9 + 3) = 24 – 12 = 12 (người)
Vậy đội trưởng đã nói đúng.
Câu 11:
Cho đoạn thẳng AB có độ dài 20cm. Trên đoạn thẳng AB lấy hai điểm C và D sao cho AC = 6cm; AD = 12cm.
a) Tính độ dài BC; CD.
b) C có phải là trung điểm của AD không? Vì sao?
 Xem đáp án
Xem đáp án
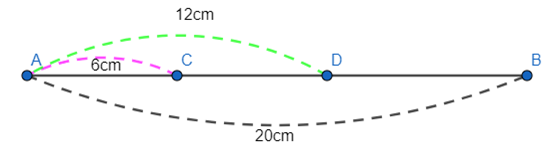
a) Vì C nằm trên đoạn thẳng AB nên AC + CB = AB
Thay số: 6 + CB = 20
CB = 20 – 6 = 14cm
Vì AC = 6cm và AD = 12 cm nên AC < AD. Do đó C nằm giữa A và D.
Ta có: AD = AC + CD
Thay số: 12 = 6 + CD
CD = 12 – 6
CD = 6cm
b) Ta có: C nằm giữa A và D.
Lại có AC = CD = AD2=122=6cm
Do đó C là trung điểm của AD
Câu 12:
 Xem đáp án
Xem đáp án
Gọi d = ƯCLN(3n +2; 5n + 3) (d ∈N∗)
Ta có: {(3n+2)⋮d(5n+3)⋮d⇒{5.(3n+2)⋮d3.(5n+3)⋮d⇒{15n+10⋮d15n+9⋮d
⇒[(15n+10)−(15n+9)]⋮d
⇔(15n+10−15n−9)⋮d
⇔1⋮d
⇒d=1
Vậy phân số đã cho tối giản.
