17 câu hỏi trắc nghiệm thuộc Đề kiểm tra Cuối kì 2 Toán 8 KNTT có đáp án (Đề 2)

Câu 1:

Với điều kiện nào của x thì phân thức $\frac{x - 5}{6 x + 24}$ có nghĩa?

A. $x \neq 2$

B. $x \neq 5$

C. $x \neq 4$

D. $x \neq - 4$

Xem đáp án

Chọn đáp án D

Câu 2:

Phương trình $a x + b = 0$ là phương trình bậc nhất một ẩn nếu

A. $a = 0$

B. $b = 0$

C. $a \neq 0$

D. $b \neq 0$

Xem đáp án

Chọn đáp án C

Câu 3:

Năm nay tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương. Gọi x là tuổi của Phương năm nay vậy thì phương trình tìm x là

A. $3 x + 13 = 2 (x + 13)$

B. $\frac{x}{3} + 13 = 2 (x + 13)$

C. $x + 13 = 2 (3 x + 13)$

D. $3 x = 2 (x + 13)$

Xem đáp án

Chọn đáp án A

Câu 4:

Giá trị của m để đồ thị hàm số y = (m – 1)x – m + 4 đi qua điểm (2;-3) là

A. $m = - 5.$

B. $m = - 3 .$

C. $m = \frac{1}{2} .$

D. $m = - \frac{1}{2} .$

Xem đáp án

Chọn đáp án A

Câu 5:

Bạn Nam tung một đồng xu cân đối và đồng chất 20 lần, có 13 lần mặt ngửa. Xác suất thực nghiệm của biến cố “Mặt sấp xuất hiện” là

A. $\frac{13}{20}$

B. $\frac{7}{20}$

C. $\frac{13}{7}$

D. $\frac{7}{13}$

Xem đáp án

Chọn đáp án B

Câu 6:

Cho tam giác DEF đồng dạng với tam giác HKI. Tỉ số nào sau đây là đúng?

A. $\frac{D E}{H K} = \frac{D F}{K I}$

B. $\frac{D E}{H K} = \frac{E F}{H I}$

C. $\frac{E F}{K I} = \frac{D F}{H I}$

D. $\frac{D F}{H I} = \frac{E F}{H K}$

Xem đáp án

Chọn đáp án C

Câu 7:

Cho hình vẽ:

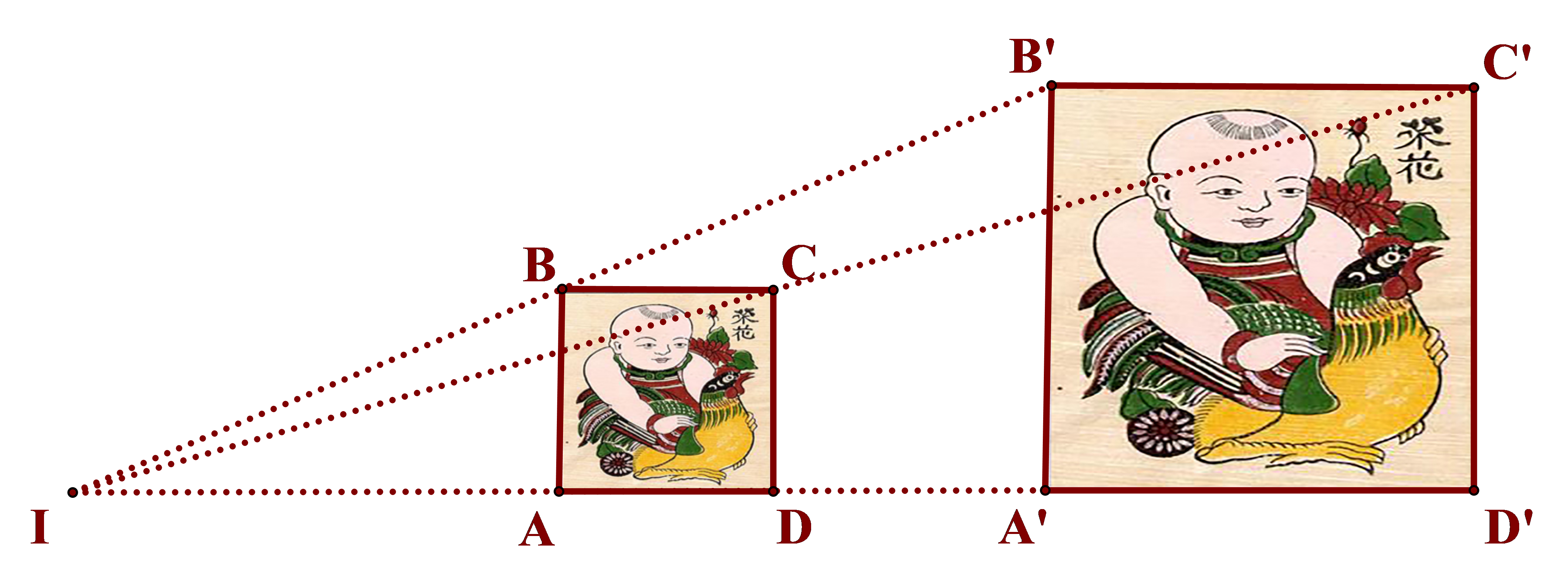
Biết các điểm A, B, C, D lần lượt là trung điểm của các đoạn thẳng IA’, IB’, IC’, ID’.

Khẳng định nào sau đây là sai?

A. Hai tứ giác ABCD và A’B’C’D’ đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh.

B. Hai đoạn thẳng AB và A’B’ đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh.

C. Hai đoạn thẳng BB’ và AA’ đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh.

D. Hai đoạn thẳng BD và B’D’ đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh.

Xem đáp án

Chọn đáp án D

Câu 8:

Cho hình chóp tam giác đều S.ABC có chiều cao SO = 24 cm, trung đoạn SI = 25 cm Độ dài đoạn OI là

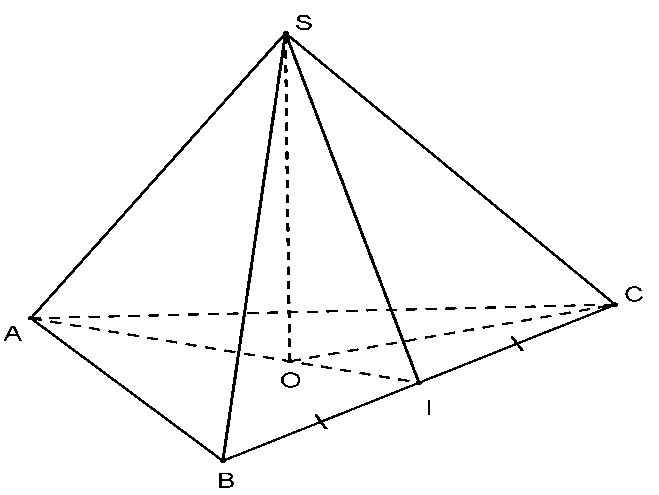
Cho hình chóp tam giác đều S.ABC có chiều cao SO = 24 cm, trung đoạn SI = 25 cm Độ dài đoạn OI là (ảnh 1)

A. 7 cm

B. 14 cm

C. 21 cm

D. 28 cm

Xem đáp án

Chọn đáp án A

Câu 9:

a) Rút gọn biểu thức P.

Xem đáp án

a) Điều kiện xác định của biểu thức P là $9 - x^{2} \neq 0,$ $x + 3 \neq 0$ hay $x \neq 3, x \neq - 3$ .

Với $x \neq 3, x \neq - 3$ ta có:

$P = \frac{x^{2} - 6 x + 9}{9 - x^{2}} + \frac{4 x + 8}{x + 3}$

$= \frac{{(x - 3)}^{2}}{(3 - x) (x + 3)} + \frac{4 x + 8}{x + 3}$

$= \frac{3 - x}{x + 3} + \frac{4 x + 8}{x + 3}$

$= \frac{3 - x + 4 x + 8}{x + 3} = \frac{3 x + 11}{x + 3}$

Vậy với $x \neq 3, x \neq - 3$ thì $P = \frac{3 x + 11}{x + 3} .$

Câu 10:

b) Tính giá trị của biểu thức P biết |x + 2| = 1.

Xem đáp án

b) Ta có $|x + 2| = 1$ suy ra $x + 2 = 1$ hoặc $x + 2 = - 1$ .

Do đó x = 1 (thỏa mãn điều kiện) hoặc x = -3 (không thỏa mãn điều kiện).

Thay x = 1 vào biểu thức P ta được:

$P = \frac{3 \cdot 1 + 11}{1 + 3} = \frac{3 + 11}{4} = \frac{7}{2} .$

Vậy $P = \frac{7}{2}$ khi $|x + 2| = 1$ .

Câu 11:

Đồng euro (EUR) là đơn vị tiền tệ chính thức ở một số quốc gia thành viên của Liên minh Châu Âu. Vào một ngày, tỉ giá hối đoái giữa đồng euro và đồng đô la Mỹ (USD) là 1 EUR = 1,1052 USD.

a) Viết công thức để chuyển đổi x euro sang y đô la Mỹ. Công thức tính y theo x này có phải là hàm số bậc nhất của x không?

b) Vào ngày đó, 200 euro có giá trị bằng bao nhiêu đô la Mỹ? 500 đô la Mỹ có giá trị bằng bao nhiêu euro?

Xem đáp án

a) Công thức để chuyển đổi x euro sang y đô la Mỹ là $y = 1,1052 x$

Công thức tính y theo x này là hàm số bậc nhất của x vì với mỗi giá trị của x, ta xác định duy nhất một giá trị của y .

b) 200 euro có giá trị là $1,1052 \cdot 200 = 210,4$ đô la Mỹ.

500 đô la Mỹ có giá trị là $500 : 1,1052 \approx 475,3$ euro.

Câu 12:

Một hộp có 25 thẻ cùng loại , mỗi thẻ được ghi một trong các số 1; 2; 3; 4; 5; ....; 25; hai thẻ khác nhau thì ghi số khác nhau.

Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:

a) “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5”;

b) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng 5”.

Xem đáp án

a) Có 5 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5” là $5; 10; 15; 20; 25.$

Do đó, xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5” là $\frac{5}{25} = \frac{1}{5}$ .

b) Có 2 kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng 5” là 14; 23.

Do đó, xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng 5” là $\frac{2}{25}$ .

Câu 13:

Để xác định chiếc điện thoại là bao nhiêu inch, các nhà sản xuất đã dựa vào độ dài đường chéo của màn hình điện thoại, biết

1 inch \approx 2,54 cm

, điện thoại có chiều rộng là 7 cm chiều dài là 15,5 cm. Hỏi chiếc điện thoại theo hình vẽ là bao nhiêu inch ? (Làm tròn kết quả đến hàng đơn vị).

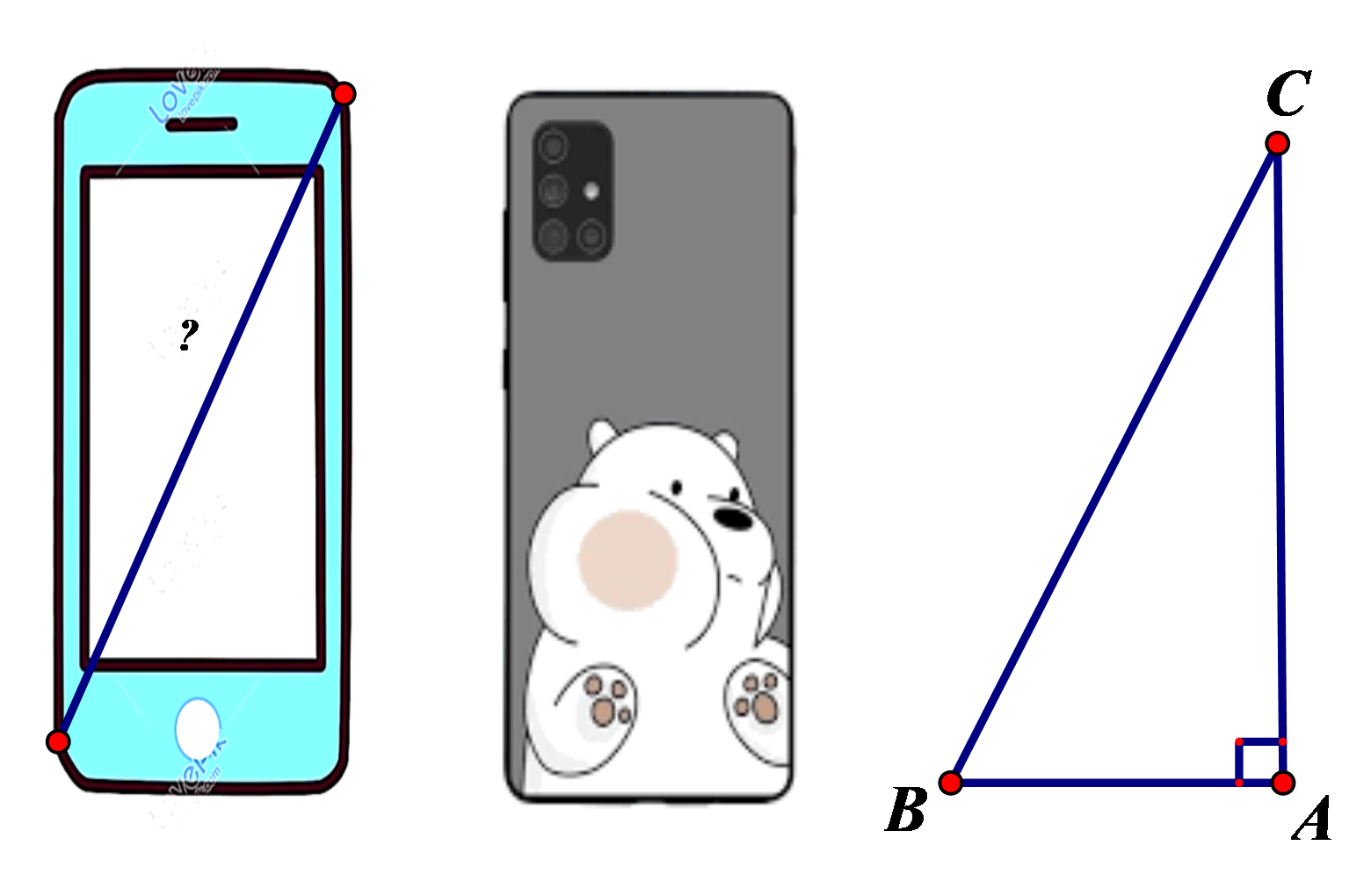
Xem đáp án

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A , ta có:

$B C^{2} = A C^{2} + A B^{2} = {(15,5)}^{2} + 7^{2} = 289,25$

Suy ra $B C = \sqrt{289,25} \approx 17 (cm)$ .

Vì $1 inch \approx 2,54 cm$ nên chiếc điện thoại theo hình vẽ có: $\frac{17}{2,54} \approx 7 (inch)$

Vậy chiếc điện thoại theo hình vẽ khoảng 7 inch

Câu 14:

Cho hình chóp tứ giác đều có chiều cao 10 cm, cạnh đáy 48 cm. Tính diện tích xung quanh của hình chóp đó.

Xem đáp án

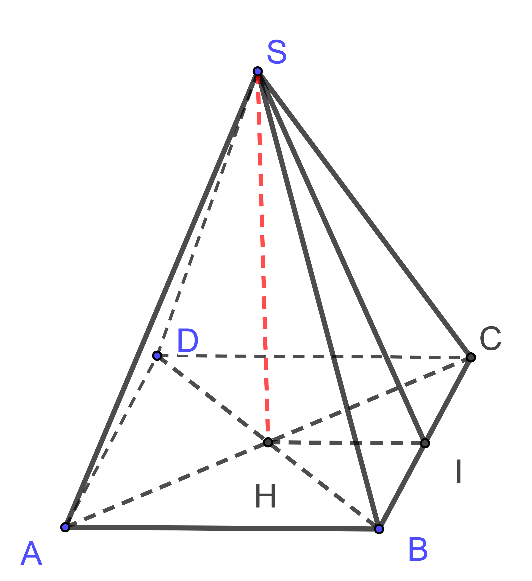
Xét hình chóp tứ giác đều S.ABCD , có đường cao SH = 10 cm, cạnh AB = 48 cm.

Gọi SI là đường cao của $Δ S B C$ .

Tam giác SBC cân tại S nên BI = IC .

Ta có HI là đường trung bình của $Δ A B C$ , nên $H I = \frac{A B}{2} = \frac{48}{2} = 24 (c m)$ .

Áp dụng định lý Pythagore vào tam giác vuông SHI , ta có :

$S I^{2} = S H^{2} + H I^{2} = 10^{2} + 24^{2} = 676 = 26^{2}$ .

Do đó SI = 26 cm.

Chu vi đáy bằng: $48 \cdot 4 = 192 (c m)$ .

$S_{x q} = p . d = \frac{192}{2} .26 = 2496 (c m^{2})$

Vậy diện tích xung quanh của hình chóp là $2496 c m^{2} .$

Câu 15:

a) Chứng minh: $Δ F H B ∽ Δ E H C$ .

b) Chứng minh: $A F \cdot A B = A E \cdot A C$ .

Xem đáp án

a) Xét $Δ F H B$ và $Δ E H C$ có:

$\hat{F H B} = \hat{E H C}$

$\hat{H F B} = \hat{H E C} (= 90 °)$

Do đó $Δ F H B ∽ Δ E H C (g.g)$ .

b) Xét $Δ A E B$ và $Δ A F C$ có:

$\hat{E A B} = \hat{F A C} (\hat{A} chung)$

$\hat{A E B} = \hat{A F C} (= 90 °)$

Do đó $Δ A E B ∽ Δ A C F (g.g)$

Suy ra

\frac{A E}{A F} = \frac{A B}{A C}

hay

A F \cdot A B = A E \cdot A C

(đpcm)

Câu 16:

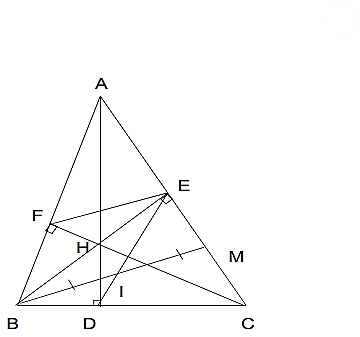
c) Đường thẳng qua B và song song với EF cắt AC tại M. Gọi I là trung điểm của BM, D là giao điểm của EI và BC. Chứng minh ba điểm A, H, D thẳng hàng.

Xem đáp án

c)

• Xét $Δ A B C$ có hai đường cao BE, CF và cắt nhau tại IH nên suy ra IH là trực tâm của tam giác ABC nên $A H ⊥ B C$ . (1)

• Xét $Δ B E M$ vuông tại E có I là trung điểm của BM nên $I E = B I = I M = \frac{B M}{2}$ .

• Xét $Δ I E M$ có IE = IM (cmt) nên tam giác IEM cân tại I .

Suy ra . $\hat{I E M} = \hat{I M E}$ (2)

• Xét $Δ A B C$ có FE // BC suy ra $\hat{A E F} = \hat{A M B}$ (hai góc đồng vị). (3)

• Ta có $A F \cdot A B = A E \cdot A C$ suy ra $\frac{A F}{A C} = \frac{A E}{A B}$ .

• Xét $Δ A B F$ và $Δ A B C$ có:

$\hat{E A F} = \hat{B A C} (\hat{A} chung)$

$\frac{A F}{A C} = \frac{A E}{A B} (cmt)$

Do đó $Δ A E F ∽ Δ A B C (c.g.c)$ .

Suy ra $\hat{A E F} = \hat{A B C}$ (hai góc tương ứng). (4)

Từ (2), (3), (4) suy ra $\hat{C E D} = \hat{A B C}$ .

• Xét $Δ C E D$ và $Δ C B A$ có:

$\hat{E C D} = \hat{B C A} (\hat{C} chung)$

$\frac{C E}{C D} = \frac{C B}{C A} (cmt)$

Do đó $Δ C E B ∽ Δ C D A (c.g.c)$ .

Suy ra $\frac{C E}{C B} = \frac{C D}{C A}$ hay $\frac{C E}{C D} = \frac{C B}{C A}$ .

• Xét $Δ C E B$ và $Δ C D A$ có:

$\frac{C E}{C D} = \frac{C B}{C A} (cmt)$

$\hat{E C B} = \hat{D C A} (\hat{C} chung)$

Do đó $Δ C E B ∽ Δ C D A (c.g.c)$ .

Suy ra $\hat{C D A} = \hat{C E B}$ (hai góc tương ứng).

Nên $\hat{C D A} = 90 °$ , do đó $A D ⊥ B C$ . (5)

Từ (1) và (5) suy ra ba điểm A, H, D thẳng hàng. (đpcm).

Câu 17:

Các biểu thức x + y + z hay $\frac{1}{x} + \frac{1}{y} + \frac{1}{z}$ có thể cùng có giá trị bằng 0 được hay không?

Xem đáp án

Giả sử $x + y + z = 0$ và $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 0.$

Ta có $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{x y + y z + z x}{x y z} .$

Mà $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 0$ nên $x + y + z = 0$ .

Từ $x + y + z = 0$ suy ra ${(x + y + z)}^{2} = 0$ hay $x^{2} + y^{2} + z^{2} + 2 (x y + y z + z x) = 0.$

Vì $x y + y z + z x = 0$ nên $x^{2} + y^{2} + z^{2} = 0$ , suy ra $x = y = z = 0.$ Điều này vô lí vì khi đó $\frac{1}{x}, \frac{1}{y}, \frac{1}{z}$ không xác định.

Vậy các biểu thức $x + y + z$ hay $\frac{1}{x} + \frac{1}{y} + \frac{1}{z}$ không thể cùng có giá trị bằng 0.

Đề kiểm tra Cuối kì 2 Toán 8 KNTT có đáp án

Đề kiểm tra Cuối kì 2 Toán 8 KNTT có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương