Giải SGK Toán 8 (Chân trời sáng tạo) Bài 4: Phân tích đa thức thành nhân tử

Giải Toán 8 Bài 4: Phân tích đa thức thành nhân tử

Giải Toán 8 trang 23 Tập 1

Khởi động trang 23 Toán 8 Tập 1: Phát biểu của bạn nữ: “99³ – 99 chia hết cho cả ba số 98, 99 và 100.”

Phát biểu của bạn nam: “Đúng rồi. Vì n³ – n chia hết cho n, n – 1 và n + 1 mà. (n là số tự nhiên, n > 1)”

Phát biểu của hai bạn có đúng không? Vì sao?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Ta có: 99³ – 99 = 99.(99² – 1)

                          = 99.(99² – 1²)

                          = 99.(99 – 1).(99 + 1)

                          = 99.98.100

Do đó 99³ – 99 chia hết cho cả ba số 98, 99 và 100.

Ta có: n³ – n = n(n² – 1)

                     = n.(n – 1).(n + 1)

Do đó n³ – n chia hết cho n, n – 1 và n + 1.

Vậy phát biểu của cả hai bạn đều đúng.

1. Phương pháp đặt nhân tử chung

Khám phá 1 trang 23 Toán 8 Tập 1: Tính diện tích của nền nhà có bản vẽ sơ lược như Hình 1 theo những cách khác nhau, biết a = 5; b = 3,5 (các kích thước tính theo mét).

Tính theo cách nào nhanh hơn?

Lời giải:

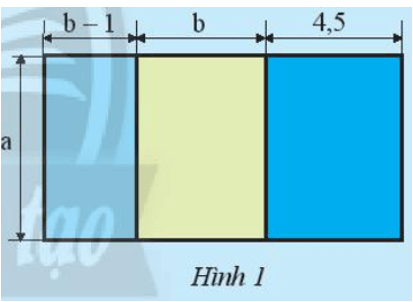
Cách 1: Tính tổng diện tích các hình.

Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b – 1 (m) là: a(b – 1) (m²).

Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b (m) là: ab (m²).

Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng 4,5 (m) là: 4,5a (m²).

Diện tích của nền nhà là: S = a(b – 1) + ab + 4,5a (m²).

Với a = 5 và b = 3,5 ta có:

S = 5.(3,5 – 1) + 5.3,5 + 4,5.5

   = 5 . (3,5 – 1 + 3,5 + 4,5)

   = 5 . 10,5

   = 52,5 (m²).

Cách 2: Tính chiều dài của nền nhà rồi tính diện tích của nền nhà.

Chiều dài của nền nhà là:

b – 1 + b + 4,5 = 2b + 3,5 (m).

Diện tích của nền nhà là: S = a.(2b + 3,5) (m²).

Với a = 5 và b = 3,5 ta có:

S = 5.(2.3,5 + 3,5) = 5 . 10,5 = 52,5 (m²).

Chú ý: Ngoài 2 cách trên ta có thể tính diện tích của nền nhà theo cách khác.

Trong tất cả các cách thì ta thấy Cách 2 là nhanh nhất.

Giải Toán 8 trang 24 Tập 1

Thực hành 1 trang 24 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) P = 6x – 2x³;

b) Q = 5x³ – 15x²y;

c) R = 3x³y³ – 6xy³z + xy.

Lời giải:

a) P = 6x – 2x³

       = 2x.3 – 2x.x²

       = 2x(3 – x²).

b) Q = 5x³ – 15x²y

       = 5x².x – 5x².3y

       = 5x²(x – 3y).

c) R = 3x³y³ – 6xy³z + xy

       = xy.3x²y² – xy.6y²z + xy.1

       = xy(3x²y² – 6y²z + 1).

2. Phương pháp sử dụng hằng đẳng thức

Khám phá 2 trang 24 Toán 8 Tập 1: Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:....

a) $4x^2-9={\left(\boxed{?}\right)}^2-{\left(\boxed{?}\right)}^2=\mathrm{...}$

b) $x^2{y}^2-\frac{1}{4}{y}^2={\left(\boxed{?}\right)}^2-{\left(\boxed{?}\right)}^2=\mathrm{...}$

Lời giải:

a) $4x^2-9={\left(\boxed{2x}\right)}^2-{\left(\boxed{3}\right)}^2=\left(2x-3\right)\left(2x+3\right)$

b) $x^2{y}^2-\frac{1}{4}{y}^2={\left(\boxed{xy}\right)}^2-{\left(\boxed{\frac{1}{2}y}\right)}^2=\left(xy-\frac{1}{2}y\right)\left(xy+\frac{1}{2}y\right)$

Thực hành 2 trang 24 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 9x² – 16;

b) 4x² – 12xy + 9y²;

c) t³ – 8;

d) 2ax³y³ + 2a.

Lời giải:

a) 9x² – 16 = (3x)² – 4²

                  = (3x – 4)(3x + 4).

b) 4x² – 12xy + 9y²

= (2x)² – 2.2x.3y + (3y)²

= (2x – 3y)².

c) t³ – 8 = t³ – 2³

              = (t – 2)(t² + t.2 + 2²)

             = (t – 2)(t² – 2t + 4).

d) 2ax³y³ + 2a

= 2a.(x³y³ + 1)

= 2a.[(xy)³ + 1³]

= 2a(xy + 1)[(xy)² – xy.1 + 1²]

= 2a(xy + 1)(x²y² – xy + 1).

Vận dụng 1 trang 24 Toán 8 Tập 1: Tìm một hình hộp chữ nhật có thể tích 2x³ – 18x (với x > 3) mà độ dài các cạnh đều là biểu thức chứa x

Lời giải:

Ta có: 2x³ – 18x = 2x(x² – 9)

                           = 2x(x² – 3²)

                           = 2x(x – 3)(x + 3)

Vậy hình hộp chữ nhật có thể tích 2x³ – 18x (với x > 3) sẽ có độ dài ba kích thước là 2x, x – 3 và x + 3.

Vận dụng 2 trang 24 Toán 8 Tập 1: Giải đáp câu hỏi ở Hoạt động khởi động (trang 23)

Lời giải:

Ta có: 99³ – 99 = 99.(99² – 1)

                          = 99.(99² – 1²)

                          = 99.(99 – 1).(99 + 1)

                          = 99.98.100

Do đó 99³ – 99 chia hết cho cả ba số 98, 99 và 100.

Ta có: n³ – n = n(n² – 1)

                     = n.(n – 1).(n + 1)

Do đó n³ – n chia hết cho n, n – 1 và n + 1.

Vậy phát biểu của cả hai bạn đều đúng.

3. Phương pháp nhóm hạng tử

Khám phá 3 trang 24 Toán 8 Tập 1: Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:

a² + ab + 2a + 2b = (a² + ab) + (2a + 2b) = …

Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?

Lời giải:

a² + ab + 2a + 2b

= (a² + ab) + (2a + 2b)

= a(a + b) + 2(a + b)

= (a + b)(a + 2).

Ta có thể biến đổi theo cách khác như sau:

a² + ab + 2a + 2b

= (a² + 2a) + (ab + 2b)

= a(a + 2) + b(a + 2)

= (a + 2)(a + b).

Giải Toán 8 trang 25 Tập 1

Thực hành 3 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) a³ – a²b + a – b;

b) x² – y² + 2y – 1.

Lời giải:

a) a³ – a²b + a – b

= (a³ – a²b) + (a – b)

= a²(a – b) + (a – b)

= (a – b)(a² + 1).

b) x² – y² + 2y – 1

= x² – (y² – 2y + 1)

= x² – (y – 1)²

= (x + y – 1).[x – (y – 1)]

= (x + y – 1)(x – y + 1).

Vận dụng 3 trang 25 Toán 8 Tập 1: Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết a = 0,8; b = 2 (các kích thước tính theo mét).

Lời giải:

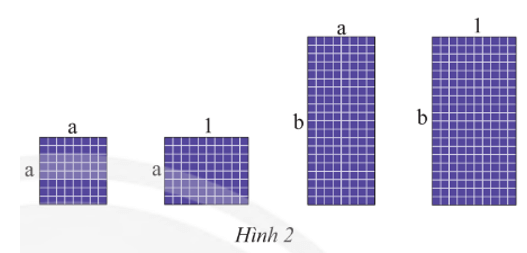
Diện tích tấm pin hình vuông có cạnh bằng a là: a² (m²).

Diện tích tấm pin hình chữ nhật có chiều dài bằng 1 và chiều rộng bằng a là: a.1 = a (m²).

Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng a là: ab (m²).

Diện tích tấm pin hình chữ nhật có chiều dài bằng b và chiều rộng bằng 1 là: b.1 = b (m²).

Tổng diện tích bốn tấm pin mặt trời là:

S = a² + a + ab + b = (a² + a) + (ab + b)

                               = a(a + 1) + b(a + 1)

                               = (a + 1)(a + b) (m²).

Vậy có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật có chiều rộng là a + 1 (m) và chiều dài là a + b (m).

Với a = 0,8 (m) và b = 2 (m) ta có:

• Chiều rộng hình chữ nhật đó là 0,8 + 1 = 1,8 (m).

• Chiều dài hình chữ nhật đó là 0,8 + 2 = 2,8 (m).

• Diện tích hình chữ nhật đó là: 1,8 . 2,8 = 5,04 (m²).

Bài tập

Bài 1 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x³ + 4x;

b) 6ab – 9ab²;

c) 2a(x – 1) + 3b(1 – x);

d) (x – y)² – x(y – x).

Lời giải:

a) x³ + 4x = x.x² + x.4 = x(x² + 4).

b) 6ab – 9ab² = 3ab.2 – 3ab.3b = 3ab(2 – 3b).

c) 2a(x – 1) + 3b(1 – x)

= 2a(x – 1) + 3b[– (x – 1)]

= 2a(x – 1) – 3b(x – 1)

= (x – 1)(2a – 3b).

d) (x – y)² – x(y – x)

= (x – y)² + x(x – y)

= (x – y)(x – y + x)

= (x – y)(2x – y).

Bài 2 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 4x² – 1;

b) (x + 2)² – 9;

c) (a + b)² – (a – 2b)².

Lời giải:

a) 4x² – 1 = (2x)² – 1² = (2x + 1)(2x –1).

b) (x + 2)² – 9 = (x + 2)² – 3²

                       = (x + 2 + 3)(x + 2 – 3)

                       = (x + 5)(x – 1).

c) (a + b)² – (a – 2b)²

= [(a + b) + (a – 2b)] . [(a + b) – (a – 2b)]

= [a + b + a – 2b] . [a + b – a + 2b]

= (2a – b).3b.

Bài 3 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 4a² + 4a + 1;

b) –3x² + 6xy – 3y²;

c) (x + y)² – 2(x + y)z + z².

Lời giải:

a) 4a² + 4a + 1

= (2a)² + 2.2a.1 + 1²

= (2a + 1)².

b) –3x² + 6xy – 3y²

= –3(x² – 2xy + y²)

= –3(x – y)².

c) (x + y)² – 2(x + y)z + z²

= [(x + y) – z]²

= (x + y – z)².

Bài 4 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 8x³ – 1;

b) x³ + 27y³;

c) x³ – y⁶.

Lời giải:

a) 8x³ – 1

= (2x)³ – 1³

= (2x – 1)[(2x)² + 2x.1 + 1²]

= (2x – 1)(4x² + 2x + 1).

b) x³ + 27y³

= x³ + (3y)³

= (x + 3y)[x² – x.3y + (3y)²]

= (x + 3y)(x² – 3xy + 9y²).

c) x³ – y⁶

= x³ – (y²)³

= (x – y²)[x² + x.y² + (y²)²]

= (x – y²)(x² + xy² + y⁴).

Bài 5 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) 4x³ – 16x;

b) x⁴ – y⁴;

c) xy² + x²y + $\frac{1}{4}$y³;

d) x² + 2x – y² + 1.

Lời giải:

a) 4x³ – 16x

= 4x(x² – 4)

= 4x(x² – 2²)

= 4x(x + 2)(x – 2).

b) x⁴ – y⁴

= (x²)² – (y²)²

= (x² + y²)(x² – y²)

= (x² + y²)(x + y)(x – y).

c) xy² + x²y + $\frac{1}{4}$y³

= y(xy + x² + $\frac{1}{4}$y²)

$=y\left[x^2+2.x.\frac{1}{2}y+{\left(\frac{1}{2}y\right)}^2\right]$

$=y{\left(x+\frac{1}{2}y\right)}^2$.

d) x² + 2x – y² + 1

= (x² + 2x + 1) – y²

= (x + 1)² – y²

= (x + 1 + y)(x + 1 – y).

Bài 6 trang 25 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x² – xy + x – y;

b) x² + 2xy – 4x – 8y;

c) x³ – x² – x + 1.

Lời giải:

a) x² – xy + x – y

= (x² – xy) + (x – y)

= x(x – y) + (x – y)

= (x – y)(x + 1).

b) x² + 2xy – 4x – 8y

= (x² + 2xy) – (4x + 8y)

= x(x +  2y) – 4(x + 2y)

= (x +  2y)(x – 4).

c) x³ – x² – x + 1

= (x³ – x²) – (x – 1)

= x²(x – 1) – (x – 1)

= (x – 1)(x² – 1)

= (x – 1)(x + 1)(x – 1)

= (x – 1)²(x + 1).

Bài 7 trang 25 Toán 8 Tập 1: Cho y > 0. Tìm độ dài cạnh của hình vuông có diện tích bằng 49y² + 28y + 4.

Lời giải:

Giả sử hình vuông có độ dài cạnh bằng a (a > 0), khi đó diện tích của hình vuông là a².

Tức là 49y² + 28y + 4 = a².

Ta phân tích đa thức 49y² + 28y + 4 thành nhân tử có dạng a².

49y² + 28y + 4

= (7y)² + 2.7y.2 + 2²

= (7y + 2)²

Vậy độ dài cạnh của hình vuông có diện tích bằng 49y² + 28y + 4 là 7y + 2.

Xem thêm lời giải bài tập SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Các phép toán với đa thức nhiều biến

Bài 3: Hằng đẳng thức đáng nhớ

Bài 5: Phân thức đại số

Bài 6: Cộng, trừ phân thức

Bài 7: Nhân, chia phân thức