Giải SBT Toán 6 (Chân trời sáng tạo) Bài 7: Số đo góc. Các góc đặc biệt

Sách bài tập Toán 6 Bài 7: Số đo góc. Các góc đặc biệt

Bài 1 trang 101 sách bài tập Toán lớp 6 Tập 2: Nhìn hình vẽ đọc số đo các góc xOt; tOt’; xOy

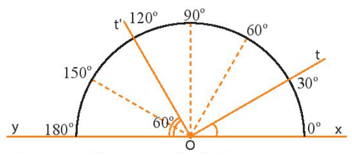
Lời giải:

Mỗi góc có 2 tia lần lượt cắt hình cung tròn tại hai vị trí có ghi số độ tương ứng.

Số đo mỗi góc = số độ lớn – số độ nhỏ.

Số đo góc xOt là: ∠xOt = 30^o – 0^o = 30^o.

Số đo góc tOt’ là: ∠tOt' = 120o – 30^o = 90^o.

Số đo góc xOy là: ∠xOy = 180o – 0^o = 180^o.

Vậy số đo các góc là: ∠xOt = 30^o; ∠tOt' = 90^o; ∠xOy = 180^o.

Bài 2 trang 101 sách bài tập Toán lớp 6 Tập 2: Những phát biểu nào sau đây là đúng?

a) Một góc có số đo nhỏ hơn số đo góc tù là góc nhọn.

b) Góc có số đo nhỏ hơn số đo góc bẹt là góc tù.

c) Góc có số đo bằng một phần hai số đo của góc tù là góc nhọn.

d) Tổng số đo của hai góc nhọn thì lớn hơn số đo của góc vuông.

e) Hai lần số đo của góc nhọn nhỏ hơn góc tù.

g) Góc có số đo lớn hơn góc vuông là góc tù.

Lời giải:

a) Sai. Vì góc vuông cũng có số đo nhỏ hơn góc tù.

b) Sai. Vì góc nhọn, góc vuông cũng có số đo nhỏ hơn góc bẹt.

c) Đúng. Góc có số đo bằng một phần hai góc tù tức là nhỏ hơn 90^o, là góc nhọn.

d) Sai. Chẳng hạn: hai góc có số đo là: 20^o và 25^o.

Tổng số đo của hai góc này là: 20^o + 25^o = 45^o < 90^o, nên nó là góc nhọn.

e) Sai. Chẳng hạn: góc có số đo bằng 60^o là góc nhọn.

Hai lần số đo góc này là: 2 . 60^o = 120^o > 90^o, nên nó là góc tù.

g) Sai. Chẳng hạn: góc bẹt có số đo lớn hơn góc vuông nhưng không phải góc tù.

Vậy phát biểu c) đúng.

Bài 3 trang 101 sách bài tập Toán lớp 6 Tập 2: Hình vẽ sau có bao nhiêu góc? Hãy đọc tên và kí hiệu các góc đó.

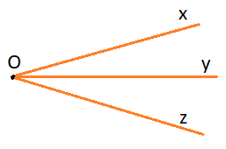
Lời giải:

Trong hình vẽ trên có:

- Đỉnh O.

- Các tia: Ox, Oy, Oz.

Có 3 góc: góc xOy; góc yOz; góc xOz.

Kí hiệu: ∠xOy , ∠yOz, ∠xOz.

Bài 4 trang 101 sách bài tập Toán lớp 6 Tập 2: Cho tia Ox như hình vẽ. Hãy vẽ tia Oy và Oz sao cho ∠xOy = 70⁰, ∠xOz = 100⁰ . Dùng thước đo góc xác định số đo của góc ∠yOz.

Lời giải:

Cách vẽ ∠xOy = 70⁰:

- Chấm điểm O trên giấy, vẽ một tia Ox tuỳ ý.

- Đặt thước đo góc sao cho tâm của thước trùng vào điểm O và vạch chỉ số 0o trùng với tia Ox.

- Nhìn trên vạch chỉ vào số 70^o, nối O với vị trí đó, ta có tia Oy sao cho ∠xOy = 70⁰.

Trường hợp 1: Tia Oy nằm giữa hai tia Ox và Oz.

Vẽ tia ∠xOz = 100⁰ sao cho Oy nằm giữa hai tia Ox và Oz (như hình vẽ).

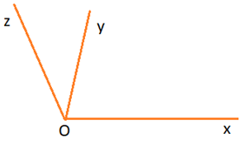
Dùng thước đo góc, ta xác định được số đo của ∠yOz = 30⁰ .

Trường hợp 2: Tia Ox nằm giữa hai tia Oy và Oz.

Vẽ tia ∠xOz = 100⁰ sao cho Ox nằm giữa hai tia Oy và Oz (như hình vẽ).

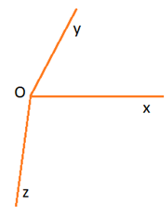
Dùng thước đo góc, ta xác định được số đo của ∠yOz = 170⁰ .

Bài 5 trang 101 sách bài tập Toán lớp 6 Tập 2: Nhìn vào hình vẽ, em hãy dự đoán có cặp góc nào bằng nhau không. Sau đó dùng dụng cụ đo góc để kiểm tra.

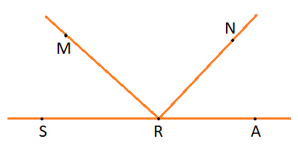
Lời giải:

* Dự đoán: ∠ARN = ∠SRM.

* Dùng thước đo góc kiểm tra hai góc: ∠ARN và ∠SRM:

- Đo ∠ARN:

+ Đặt thước đo góc sao cho tâm của thước trùng vào điểm R và vạch chỉ số 0^o trùng với tia RA.

+ Nhìn tia RN trùng với vạch chỉ bao nhiêu độ thì đó chính là số đo của ∠ARN.

- Đo ∠SRM:

+ Đặt thước đo góc sao cho tâm của thước trùng vào điểm R và vạch chỉ số 0^o trùng với tia RS.

+ Nhìn tia RM trùng với vạch chỉ bao nhiêu độ thì đó chính là số đo của ∠SRM.

- Sau đó so sánh số đo hai góc, ta được: ∠ARN = ∠SRM.

Bài 6 trang 102 sách bài tập Toán lớp 6 Tập 2: Nhìn vào các hình vẽ dưới đây, em hãy chỉ ra đâu là góc tù, góc bẹt, góc nhọn và góc vuông.

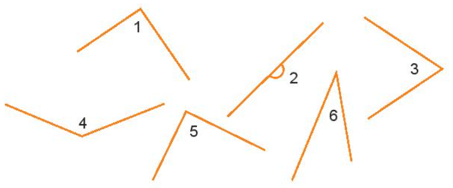
Lời giải:

- Góc vuông là góc có số đo 90^o.

- Góc nhọn là góc có số đo lớn hơn 0^o và nhỏ hơn 90^o.

- Góc tù là góc có số đo lớn hơn 90^o và nhỏ hơn 180^o.

Nhìn vào các hình trên, ta có:

- Các góc hình 1 và 5 là góc vuông;

- Góc ở hình 2 là góc bẹt;

- Các góc hình 3 và 6 là góc nhọn;

- Góc ở hình 4 là góc tù.

Bài 7 trang 102 sách bài tập Toán lớp 6 Tập 2: Một tấm nhựa được thiết kế như hình dưới đây. Có thể dùng tấm nhựa để đo độ lớn của các góc không? Vì sao?

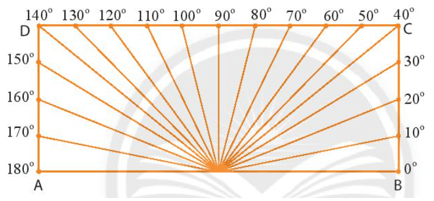
Lời giải:

Không sử dụng tấm nhựa này để đo góc được.

Vì các góc số đo không phải tròn trục, chẳng hạn 45^o, 125^o, 148^o thì việc sử dụng dụng cụ này sẽ đo không chính xác.

Bài 8 trang 102 sách bài tập Toán lớp 6 Tập 2: Chỉ dùng thước kẻ để vẽ các góc 30^o, 45^o, 60^o và 90^o. Sau đó, dùng thước đo góc để kiểm tra tính chính xác góc vừa vẽ.

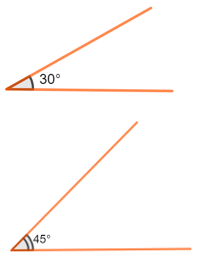
Lời giải:

Ta có thể tận dụng dòng kẻ của vở hoặc hoặc hai mép của thước thẳng để vẽ góc có số đo 90^o (góc vuông).

Từ góc 90^o, ta có thể ước lượng để vẽ được số đo của các góc 30^o, 45^o, 60^o dựa vào các tỉ số sau:

Góc có số đo 30^o thì bằng 1/3 số đo của góc 90^o.

(Chia góc có số đo bằng 90o thành 3 phần bằng nhau, ta lấy 1 phần thì được số đo của góc 30^o).

Góc có số đo 45^o thì bằng 1/2 số đo của góc 90o.

(Chia góc có số đo bằng 90^o thành 2 phần bằng nhau, ta lấy 1 phần thì được số đo của góc 45^o).

Góc có số đo 60^o thì bằng 2/3 số đo của góc 90^o.

(Chia góc có số đo bằng 90^o thành 3 phần bằng nhau, ta lấy 2 phần thì được số đo của góc 60^o).

Thử vẽ các góc này bằng thước kẻ thông thường, sau đó dùng thước đo góc để kiểm tra lại.

Hình minh họa.

Xem thêm các bài giải SBT Toán 6 Chân trời sáng tạo hay, chi tiết khác:

Bài 5: Trung điểm của đoạn thẳng

Bài 6: Góc

Bài tập cuối chương 8

Bài 1: Phép thử nghiệm - Sự kiện

Bài 2: Xác suất thực nghiệm