Sách bài tập Toán 6 Bài 2: Xác suất thực nghiệm

Hãy tính xác suất thực nghiệm của các sự kiện:
a) Gieo được đỉnh ghi số 2.
b) Gieo được đỉnh ghi số lẻ.
Lời giải:
a) Số lần gieo được đỉnh ghi số 2 là: 6;
Tổng số lần gieo là : 24.
Vậy xác suất thực nghiệm của sự kiện “Gieo được đỉnh ghi số 2” là: 6/24 = 0,25
b) Các số lẻ xuất hiện trong các lần gieo là 1 và 3.
Số lần gieo được đỉnh ghi số 1 là: 5;
Số lần gieo được đỉnh ghi số 3 là: 6.
Số lần gieo được đỉnh ghi số lẻ (tức là số lần gieo ghi đỉnh số 1 hoặc số 3) là: 5+ 6 = 11.
Tổng số lần gieo là: 24.
Vậy xác suất thực nghiệm của sự kiện “Gieo được đỉnh ghi số lẻ” là: 11/24

Hãy tính xác suất thực nghiệm của các sự kiện:
a) Một ngày có đúng 3 bạn đi học muộn.
b) Một ngày không có bạn nào đi học muộn.
c) Một ngày có bạn đi học muộn.
Lời giải:
a) Số ngày có đúng 3 bạn đi học muộn trong 20 ngày là: 1.
Vậy xác suất thực nghiệm của sự kiện “Một ngày có đúng 3 bạn đi học muộn” là: 1/20 = 0,05
b) Số ngày không có bạn nào đi học muộn trong 20 ngày là: 10.
Vậy xác suất thực nghiệm của sự kiện “Một ngày không có bạn nào đi học muộn” là: 10/20 = 0,5
c) Số ngày có bạn đi học muộn (nghĩa là có thể có 1 bạn đi học muộn hoặc 2 bạn đi học muộn hoặc 3 bạn đi học muộn) trong 20 ngày là: 10.
Vậy xác suất thực nghiệm của sự kiện “Một ngày có bạn đi học muộn” là: 10/20 = 0,5

Hãy tính xác suất thực nghiệm của sự kiện:
a) Thảo lấy được thẻ ghi số chẵn.
b) Thảo lấy được thẻ ghi số nguyên tố.
Lời giải:
a) Các thẻ số chẵn trong bảng trên là: thẻ ghi số 2 và số 4.
Số lần Thảo lấy được thẻ ghi số 2 là: 5.
Số lần Thảo lấy được thẻ ghi số 4 là: 5.
Số lần Thảo lấy được thẻ ghi số chẵn (thẻ ghi số 2 hoặc số 4) trong 20 lần là: 5 + 5 = 10
Vậy xác suất thực nghiệm của sự kiện “Thảo lấy được thẻ ghi số chẵn” là: 10/20 = 0,5
b) Các thẻ số nguyên tố trong bảng trên là: thẻ ghi số 2 và số 3.
Số lần Thảo lấy được thẻ ghi số 2 là 5.
Số lần Thảo lấy được thẻ ghi số 3 là 5.
Số lần Thảo lấy được thẻ ghi số nguyên tố (thẻ ghi số 2 hoặc số 3) trong 20 lần là: 5 + 5 = 10.

Hãy tính xác suất thực nghiệm của các sự kiện sau trong mỗi lần bắn:
a) Xạ thủ bắn được 10 điểm.
b) Xạ thủ bắn được ít nhất 8 điểm.
Lời giải:
a) Số lần xạ thủ bắn được 10 điểm trong 20 lần bắn là: 5
Vậy xác suất thực nghiệm của sự kiện “Xạ thủ bắn được 10 điểm” là: 5/20 = 0,25
b) Số lần xạ thủ bắn được ít nhất 8 điểm là số lần xạ thủ bắn được là 8 điểm hoặc hơn 8 điểm.
Do đó số lần xạ thủ bắn được ít nhất 8 điểm bằng tổng số lần bắn được 8 điểm, 9 điểm và 10 điểm.
Số lần xạ thụ bắn xạ thủ bắn được 8 điểm là: 5.
Số lần xạ thụ bắn xạ thủ bắn được 9 điểm là: 6.
Số lần xạ thụ bắn xạ thủ bắn được 10 điểm là: 5.
Số lần xạ thủ bắn được ít nhất 8 điểm trong 20 lần bắn là: 5 + 6 + 5 = 16
Vậy xác suất thực nghiệm của sự kiện “Xạ thủ bắn được ít nhất 8 điểm” là: 16/20 = 0,8

Hãy tính xác suất thực nghiệm của sự kiện:
a) Có một đồng xu sấp, một đồng xu ngửa.
b) Hai đồng xu đều sấp.
Lời giải:
a) Số lần tung được một đồng xu sấp, một đồng xu ngửa trong 100 lần tung là: 48.
Vậy xác suất thực nghiệm của sự kiện “Có một đồng xu sấp, một đồng xu ngửa” là: 48/100 = 0.48
b) Số lần tung được hai đồng xu sấp trong 100 lần tung là: 20.
Vậy xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp” là: 20/100 = 0,2
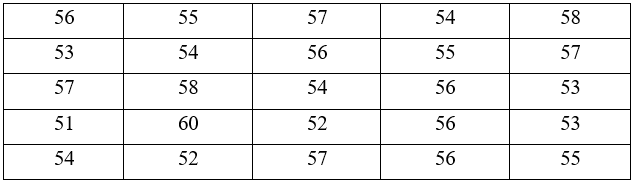
Hãy tính xác suất thực nghiệm của sự kiện:
a) Thửa ruộng được chọn có năng suất 55 tạ/ha.
b) Thửa ruộng được chọn có năng suất không quá 55 tạ/ha.
Lời giải:
a) Số thửa ruộng đạt 55 tạ/ha trong 25 thửa ruộng được chọn là: 3.
Vậy xác suất thực nghiệm của sự kiện “Thửa ruộng được chọn có năng suất 55 tạ/ha” là: 3/25 = 0,12
b) Các thửa ruộng đạt không quá 55 tạ/ha là các thửa ruộng có năng suất 55 tạ/ha hoặc nhỏ hơn 55 tạ/ha.
Do đó số thửa ruộng đạt không quá 55 tạ/ha bằng tổng các thửa ruộng có năng suất đạt 51 tạ/ha, 52 tạ/ha, 53 tạ/ha, 54 tạ/ha và 55 tạ/ha.
Số thửa ruộng đạt 51 tạ/ha là 1.
Số thửa ruộng đạt 52 tạ/ha là 2.
Số thửa ruộng đạt 53 tạ/ha là 3.
Số thửa ruộng đạt 54 tạ/ha là 4.
Số thửa ruộng đạt 55 tạ/ha là 3.
Do đó số thửa ruộng đạt không quá 55 tạ/ha trong 25 thửa ruộng được chọn là: 1+ 2 + 3 + 4 + 3 = 13.
Vậy xác suất thực nghiệm của sự kiện “Thửa ruộng được chọn có năng suất không quá 55 tạ/ha” là: 13/25 = 0,52

Hãy tính xác suất thực nghiệm của sự kiện:
a) Cửa hàng bán được 7 xe máy một ngày.
b) Cửa hàng bán được trên 5 xe máy một ngày.
Lời giải:
a) Số ngày cửa hàng bán được 7 xe máy trong 30 ngày là 6.
Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được 7 xe máy một ngày” là: 6/30 = 0,2
b) Số ngày cửa hàng bán được trên 5 xe máy bằng tổng số các ngày cửa hàng bán được 6 xe máy, 7 xe máy, 8 xe máy, 9 xe máy và 12 xe máy.
Số ngày cửa hàng bán được 6 xe máy là: 2.
Số ngày cửa hàng bán được 7 xe máy là: 6.
Số ngày cửa hàng bán được 8 xe máy là: 3.
Số ngày cửa hàng bán được 9 xe máy là: 3.
Số ngày cửa hàng bán được 12 xe máy là: 1
Số ngày cửa hàng bán được trên 5 xe máy trong 30 ngày là:
2 + 6 + 3 + 3 + 1 = 15.
Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được trên 5 xe máy một ngày” là: 15/30 = 0,5
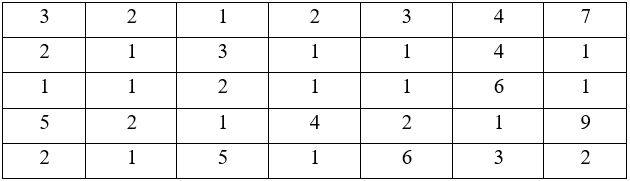
Hãy tính xác suất thực nghiệm của sự kiện:
a) Một bạn chỉ cần gieo một lần đã được mặt sấp.
b) Một bạn phải gieo ít nhất 3 lần mới được mặt sấp.
Lời giải:
Tổng số học sinh cả lớp là: 35.
a) Số bạn chỉ cần gieo một lần đã được mặt sấp là: 14.
Vậy xác suất thực nghiệm của sự kiện “Một bạn chỉ cần gieo một lần đã được mặt sấp” là: 14/35 = 0,4
b) Số bạn phải gieo ít nhất 3 lần mới được mặt sấp là: 13.
Vậy xác suất thực nghiệm của sự kiện “Một bạn phải gieo ít nhất 3 lần mới được mặt sấp” là: 13/35
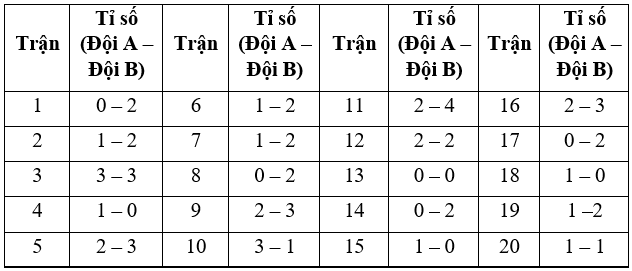
Hãy tính xác suất thực nghiệm của sự kiện sau trong mỗi trận đấu:
a) Đội A thắng đội B.
b) Hai đội hoà nhau.
c) Đội B ghi được hơn 1 bàn thắng.
d) Tổng số bàn thắng hai đội ghi được lớn hơn 2.
Lời giải:
a) Số trận mà đội A thắng đội B trong 20 trận gần đây là: 4 (là trận 4, trận 10, trận 15 và trận 18).
Vậy xác suất thực nghiệm của sự kiện “Đội A thắng đội B” là: 4/20 = 0,2
b) Số trận mà hai đội hoà nhau trong 20 trận gần đây là: 4 (là trận 3, trận 12, trận 13 và trận 20).
Vậy xác suất thực nghiệm của sự kiện “Hai đội hoà nhau” là: 4/20 = 0,2
c) Số trận mà đội B ghi được hơn 1 bàn thắng trong 20 trận gần đây là: 14 (Trừ các trận 4, trận 10, trận 13, trận 15, trận 18 và trận 20).
Vậy xác suất thực nghiệm của sự kiện “Đội B ghi được hơn 1 bàn thắng” là: 14/20 = 0,7
d) Số trận mà hai đội ghi được số bàn thắng lớn hơn 2 trong 20 trận gần đây là: 11 (là trận 2, trận 3, trận 5, trận 6, trận 7, trận 9, trận 10, trận 11, trận 12, trận 16 và trận 19).
Vậy xác suất thực nghiệm của sự kiện “Tổng số bàn thắng hai đội ghi được lớn hơn 2” là: 11/20 = 0,55
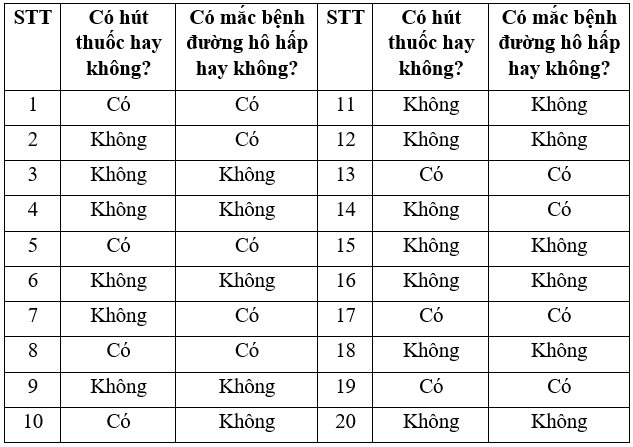
Hãy tính xác suất thực nghiệm của sự kiện:
a) Người được hỏi có hút thuốc.
b) Người được hỏi không mắc bệnh đường hô hấp.
c) Người được hỏi có hút thuốc và bị mắc bệnh đường hô hấp.
d) Người được hỏi không hút thuốc và không mắc bệnh đường hô hấp.
Lời giải:
a) Số người có hút thuốc trong số 20 người được hỏi là: 7.
Vậy xác suất thực nghiệm của sự kiện “Người được hỏi có hút thuốc” là: 7/20 = 0,35
b) Số người không mắc bệnh đường hô hấp trong số 20 người được hỏi là: 11.
Vậy xác suất thực nghiệm của sự kiện “Người được hỏi không mắc bệnh đường hô hấp” là: 11/20 = 0,55
c) Số người có hút thuốc và bị mắc bệnh đường hô hấp trong số 20 người được hỏi là: 6.
Vậy xác suất thực nghiệm của sự kiện “Người được hỏi có hút thuốc và bị mắc bệnh đường hô hấp” là: 6/20 = 0,3
d) Số người không hút thuốc và không mắc bệnh đường hô hấp trong số 20 người được hỏi là: 3.
Vậy xác suất thực nghiệm của sự kiện “Người được hỏi không hút thuốc và không mắc bệnh đường hô hấp” là: 3/20 = 0,15
Xem thêm các bài giải SBT Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 7: Số đo góc. Các góc đặc biệt
Bài 1: Phép thử nghiệm - Sự kiện

