Giải SBT Toán 6 (Cánh diều) Bài 4: Xác suất thực nghiệm trong một số trò chơi và thí nghiệm đơn giản

Sách bài tập Toán 6 Bài 4: Xác suất thực nghiệm trong một số trò chơi và thí nghiệm đơn giản

Bài 18 trang 17 sách bài tập Toán lớp 6 Tập 2: Một hộp có chứa ba quả cầu có kích thước và khối lượng như nhau, ghi các chữ a, b, c như Hình 11.

a) Lấy ngẫu nhiên một quả cầu trong hộp. Kí hiệu A là kết quả “Lấy được quả cầu ghi chữ a”; B là kết quả “Lấy được quả cầu ghi chữ b”; C là kết quả “Lấy được quả cầu ghi chữ c”. Hãy nhận xét về khả năng xảy ra các kết quả A, B, C nói trên.

b) Mỗi lần bạn Minh lấy ngẫu nhiên một quả cầu trong hộp, ghi lại kết quả xảy ra và bỏ lại quả cầu đó vào hộp. Trong 10 lần lấy liên tiếp, có 3 lần xuất hiện kết quả A, 2 lần xuất hiện kết quả B, 5 lần xuất hiện kết quả C. Tìm xác suất thực nghiệm đối với lần lượt từng kết quả A, B, C.

Lời giải:

a) Khi lấy ngẫu nhiên một quả cầu trong hộp có 3 quả cầu đã cho, ta có thể thu được 1 trong 3 kết quả “Lấy được quả cầu ghi chữ a” hoặc “Lấy được quả cầu ghi chữ b” hoặc “Lấy được quả cầu ghi chữ c”.

Vậy khả năng xảy ra các kết quả A, B, C là có thể.

b) ∙ Có 3 lần xuất hiện kết quả A trong 10 lần lấy liên tiếp.

Do đó xác suất thực nghiệm xảy ra kết quả A là: $\frac{3}{10}$.

∙ Có 2 lần xuất hiện kết quả B trong 10 lần lấy liên tiếp.

Do đó xác suất thực nghiệm xảy ra kết quả B là: $\frac{4}{10}=\frac{2}{5}$.

∙ Có 5 lần xuất hiện kết quả C trong 10 lần lấy liên tiếp.

Do đó xác suất thực nghiệm xảy ra kết quả A là: $\frac{5}{10}=\frac{1}{2}$.

Vậy xác suất thực nghiệm đối với kết quả A là $\frac{3}{10}$, kết quả B là $\frac{2}{5}$ và kết quả C là $\frac{1}{2}$.

Bài 19 trang 17 sách bài tập Toán lớp 6 Tập 2: Một hộp chứa bốn chiếc kẹp nơ tóc có kích thước và mẫu mã giống nhau, trong đó có 1 chiếc màu xanh, 1 chiếc màu hồng, 1 chiếc màu vàng, 1 chiếc màu nâu. Mỗi lần bạn Lan lấy ngẫu nhiên một chiếc nơ trong hộp, ghi lại màu của chiếc nơ được lấy ra và bỏ lại chiếc nơ đó vào hộp. Trong 10 lần lấy liên tiếp, có 3 lần xuất hiện màu xanh, 2 lần xuất hiện màu vàng, 4 lần xuất hiện màu hồng, 1 lần xuất hiện màu nâu. Tìm xác suất thực nghiệm xuất hiện chiếc nơ:

a) Màu xanh;

b) Màu hồng;

c) Màu vàng;

d) Màu nâu.

Lời giải:

a) Có 3 lần xuất hiện màu xanh trong 10 lần lấy liên tiếp.

Do đó xác suất thực nghiệm xuất hiện chiếc nơ màu xanh là: $\frac{3}{10}$.

b) Có 4 lần xuất hiện màu hồng trong 10 lần lấy liên tiếp.

Do đó xác suất thực nghiệm xuất hiện chiếc nơ màu hồng là: $\frac{4}{10}=\frac{2}{5}$.

c) Có 2 lần xuất hiện màu vàng trong 10 lần lấy liên tiếp.

Do đó xác suất thực nghiệm xuất hiện chiếc nơ màu vàng là: $\frac{2}{10}=\frac{1}{5}$.

d) Có 1 lần xuất hiện màu nâu trong 10 lần lấy liên tiếp.

Do đó xác suất thực nghiệm xuất hiện chiếc nơ màu nâu là: $\frac{1}{10}$.

Bài 20 trang 18 sách bài tập Toán lớp 6 Tập 2: Tung một đồng xu 15 lần liên tiếp. Hãy ghi kết quả thống kê theo mẫu sau:

Tính xác suất thực nghiệm xuất hiện:

a) Mặt N;

b) Mặt S.

Lời giải:

Ta tiến hành tung đồng xu 15 lần ta thu được các kết quả mặt N hoặc mặt S rồi điền vào bảng.

Giả sử, sau 15 lần tung ta thu được kết quả như sau:

Mặt N: mặt ngửa, S: sấp

a) Có 8 lần xuất hiên mặt N trong 15 lần tung đồng xu.

Do đó xác suất thực nghiệm xuất hiện mặt N là: $\frac{8}{15}$.

b) Có 7 lần xuất hiên mặt S trong 15 lần tung đồng xu.

Do đó xác suất thực nghiệm xuất hiện mặt S là: $\frac{7}{15}$.

Bài 21 trang 18 sách bài tập Toán lớp 6 Tập 2: Trả lời các câu hỏi sau trang 18 sách bài tập Toán lớp 6 Tập 2:

a) Nếu tung một đồng xu 12 lần liên tiếp, có 5 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?

b) Nếu tung một đồng xu 27 lần liên tiếp, có 15 lần xuất hiện mặt S thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?

c) Nếu tung một đồng xu 32 lần liên tiếp, có 17 lần xuất hiện mặt S thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?

Lời giải:

a) Có 5 lần xuất hiện mặt N khi tung một đồng xu 12 lần liên tiếp.

Do đó xác suất thực nghiệm xuất hiện mặt N là $\frac{5}{12}$.

b) Có 15 lần xuất hiện mặt S khi tung một đồng xu 27 lần liên tiếp.

Do đó xác suất thực nghiệm xuất hiện mặt S là $\frac{15}{27}=\frac{5}{9}$.

c) Có 17 lần xuất hiện mặt S khi tung một đồng xu 32 lần liên tiếp nên số lần xuất hiện mặt N là:

32 – 17 = 15 (lần)

Do đó xác suất thực nghiệm xuất hiện mặt N là $\frac{15}{32}$.

Bài 22 trang 18 sách bài tập Toán lớp 6 Tập 2: Một hộp có 5 quả cầu cùng loại, mỗi quả được ghi một trong các số nguyên dương chẵn nhỏ hơn 11, hai quả khác nhau được ghi hai số khác nhau. Lấy ngẫu nhiên một quả từ trong hộp, ghi lại số của quả được lấy ra và bỏ lại quả đó vào hộp. Sau 30 lần lấy liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:

Tính xác suất thực nghiệm xuất hiện:

a) Số 2;

b) Số 8;

c) Số 10.

Lời giải:

Lấy ngẫu nhiên một quả cầu từ trong hộp, ghi lại số của quả được lấy ra và bỏ lại quả đó vào hộp ta thu được các kết quả khác nhau. Thực hiện lấy ngẫu nhiên 30 lần liên tiếp rồi điền vào bảng.

Chẳng hạn sau 30 lần ta thu được kết quả như sau:

a) Có 6 lần xuất hiện mặt số 2 trong 30 lần lấy quả cầu.

Do đó xác suất thực nghiệm xuất hiện số 2 là: $\frac{6}{30}=\frac{1}{5}$.

b) Có 4 lần xuất hiện mặt số 8 trong 30 lần lấy quả cầu.

Do đó xác suất thực nghiệm xuất hiện số 8 là: $\frac{4}{30}=\frac{2}{15}$.

c) Có 7 lần xuất hiện mặt số 10 trong 30 lần lấy quả cầu.

Do đó xác suất thực nghiệm xuất hiện số 10 là: $\frac{7}{30}$.

Bài 23 trang 18 sách bài tập Toán lớp 6 Tập 2: Gieo một con xúc xắc 12 lần liên tiếp, bạn Na có kết quả thống kê như sau:

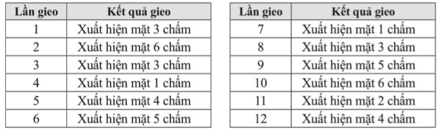
a) Hãy kiểm đếm số lần xuất hiện mặt 3 chấm và mặt 5 chấm sau 12 lần gieo.

b) Tính xác suất thực nghiệm xuất hiện mặt 3 chấm.

c) Tính xác suất thực nghiệm xuất hiện mặt 5 chấm.

Lời giải:

a) Quan sát bảng thống kê, ta kiểm đếm số lần xuất hiện mặt 3 chấm và mặt 5 chấm, dễ thấy: Số lần xuất hiện mặt 3 chấm và mặt 5 chấm lần lượt là 3 và 2.

Vậy có 3 lần xuất hiện mặt 3 chấm và 2 lần xuất hiện mặt 5 chấm sau 12 lần gieo.

b) Có 3 lần xuất hiện mặt 3 chấm sau 12 lần gieo.

Do đó xác suất thực nghiệm xuất hiện mặt 3 chấm là: $\frac{3}{12}=\frac{1}{4}$.

c) Có 2 lần xuất hiện mặt 5 chấm sau 12 lần gieo.

Do đó xác suất thực nghiệm xuất hiện mặt 5 chấm là: $\frac{2}{12}=\frac{1}{6}$.

Bài 24 trang 19 sách bài tập Toán lớp 6 Tập 2: a) Nếu gieo một xúc xắc 17 lần liên tiếp, có 6 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng bao nhiêu?

b) Nếu gieo một xúc xắc 16 lần liên tiếp, có 3 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng bao nhiêu?

Lời giải:

a) Có 6 lần xuất hiện mặt 6 chấm khi gieo một xúc xắc 17 lần liên tiếp.

Do đó xác suất thực nghiệm xuất hiện mặt 6 chấm là $\frac{6}{17}$.

b) Có 3 lần xuất hiện mặt 2 chấm khi gieo một xúc xắc 16 lần liên tiếp.

Do đó xác suất thực nghiệm xuất hiện mặt 2 chấm là $\frac{3}{16}$.

Xem thêm các bài giải SBT Toán 6 Cánh diều hay, chi tiết khác:

Bài 2: Biểu đồ cột kép

Bài 3: Mô hình xác suất trong một số trò chơi và thí nghiệm đơn giản

Bài ôn tập cuối chương 4

Bài 1: Phân số với tử và mẫu là số nguyên

Bài 2: So sánh các phân số. Hỗn số dương