Giải Chuyên đề Toán 11 Bài tập cuối chuyên đề 2
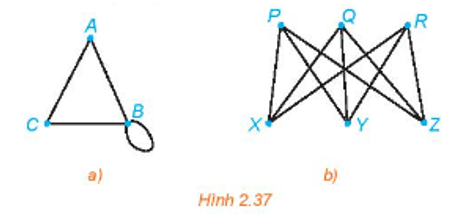
Bài 2.19 trang 50 Chuyên đề Toán 11: Viết tập hợp các đỉnh và tập hợp các cạnh của mỗi đồ thị sau:
Lời giải:
a) Với đồ thị Hình 2.37 a) ta có:
+ Tập hợp các đỉnh là V(G) = {A; B; C};
+ Tập hợp các cạnh là E(G) = {AB; AC; BC; BB}.
b) Với đồ thị Hình 2.37 b) ta có:
+ Tập hợp các đỉnh là V(G) = {P; Q; R; X; Y; Z};
+ Tập hợp các cạnh là E(G) = {PX; PY; PZ; QX; QY; QZ; RX; RY; RZ}.
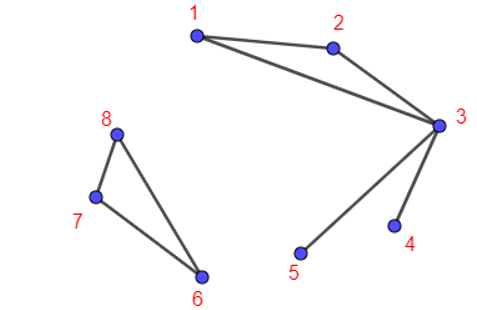
Bài 2.20 trang 50 Chuyên đề Toán 11: Vẽ đồ thị G = (V, E) với các đỉnh và các cạnh như sau:
V = {1; 2; 3; 4; 5; 6; 7; 8} và E = {12; 13; 23; 34; 35; 67; 68; 78}.
Đồ thị này có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?
Lời giải:
Ta vẽ được đồ thị G như hình trên.
Đồ thị G này không có khuyên và hai đỉnh chỉ được nối với nhau bằng nhiều nhất một cạnh nên là một đơn đồ thị.
Đồ thị G không phải đồ thị đầy đủ vì không phải tất cả các cặp đỉnh của nó đều được nối với nhau bằng một cạnh.
Lời giải:
Giả sử có đồ thị G thỏa mãn yêu cầu bài toán. Gọi x là số đỉnh bậc 3 của đồ thị.
Khi đó số đỉnh bậc 6 của đồ thì là 12 – x.
Tổng tất cả các bậc của đỉnh của đồ thị G là 3x + 6(12 – x) = 3x + 72 – 6x = 72 – 3x.
Mà đồ thị G có 28 cạnh nên tổng tất cả các bậc của đỉnh của đồ thị G bằng 28 . 2 = 56.
Do đó ta có phương trình 72 – 3x = 56, suy ra x = 163∉ℤ, mà số đỉnh phải là số nguyên nên không tồn tại đồ thị thỏa mãn điều kiện đề bài.
Vậy không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 6.
Lời giải:
Giả sử G là một đơn đồ thị có n đỉnh (n ≥ 2).
Vì G là đơn đồ thị nên mỗi đỉnh của G không có khuyên và chỉ có thể nối với các đỉnh khác không quá một cạnh, nghĩa là mỗi đỉnh của G có bậc tối đa là (n – 1) (*).
Giả sử bậc của các đỉnh của G đều khác nhau. Khi đó bậc của n đỉnh của G lần lượt là 0, 1, ..., (n – 1), nghĩa là G phải có đỉnh bậc 0.
Do G có đỉnh bậc 0 nên các đỉnh khác của G có bậc tối đa là (n – 2) (mâu thuẫn (*)).
Vậy có ít nhất 2 đỉnh của G có cùng bậc.
Lời giải:
Giả sử G là một đồ thị đầy đủ có n đỉnh và có ít nhất 1 000 cạnh (n ∈ ℕ, n ≥ 2).
Vì G là đồ thị đầy đủ nên mỗi cặp đỉnh của G đều được nối với nhau bằng một cạnh, do đó mỗi đỉnh của G đều có bậc là (n – 1).
Tổng tất cả các bậc của các đỉnh của G là n(n – 1).
Suy ra G có số cạnh là n(n−1)2.
Vì G có ít nhất 1 000 cạnh nên ta có n(n−1)2≥1000
⇔ n(n – 1) – 2 000 ≥ 0
⇔ n2 – n – 2 000 ≥ 0 (*)
Giải bất phương trình (*), ta được n≤1−3√8892≈−44,22 (không thỏa mãn) hoặc n≥1+3√8892≈45,22 (thỏa mãn).
Do n là số tự nhiên nên n nhỏ nhất thỏa mãn là 46.
Vậy số đỉnh nhỏ nhất cần thiết để có thể xây dựng một đồ thị đầy đủ với ít nhất 1 000 cạnh là 46 đỉnh.
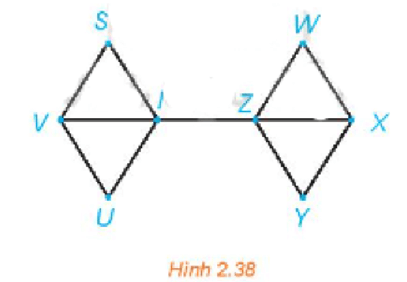
Lời giải:
Năm đường đi từ S đến Y trong đồ thị trên Hình 2.38 là SVUIZY; SVIZY; SIZY; SIZWWXY; SIZXY.
Lời giải:
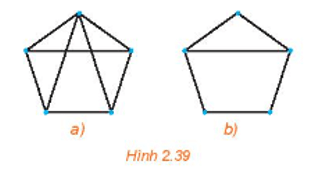
Ta thấy hai đồ thị ở Hình 2.39 đều là đơn đồ thị và mỗi đồ thị đều có số đỉnh lớn hơn 3.
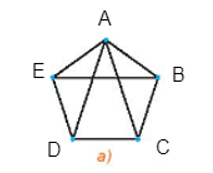
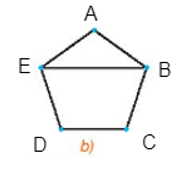
+) Đối với Hình 2.39 a), đặt tên các đỉnh như hình vẽ:
Đồ thị này có 5 đỉnh, các đỉnh đều có bậc là 3, trừ đỉnh A có bậc là 4 nên mỗi cặp đỉnh không kề nhau có tổng bậc nhỏ nhất là 6, mà 6 > 5, do đó đồ thị này thỏa mãn định lí Ore. Vậy đồ thị Hình 2.39 a) có một chu trình Hamilton.
+) Đối với Hình 2.39 a), đặt tên các đỉnh như hình vẽ:
Đồ thị này có 5 đỉnh, đỉnh E và đỉnh B đều có bậc là 3, các đỉnh còn lại đều có bậc là 2 nên mỗi cặp đỉnh không kề nhau có tổng số bậc nhỏ nhất là 4 (chẳng hạn đỉnh A và đỉnh D), do đó đồ thị này không thỏa mãn định lí Ore. Tuy nhiên thì đồ thị này vẫn có chu trình Hamilton, một chu trình Hamilton của đồ thị là ABCDEA.
Do đó, ta khẳng định lại định lí Ore chỉ là một điều kiện đủ cho sự tồn tại của chu trình Hamilton.
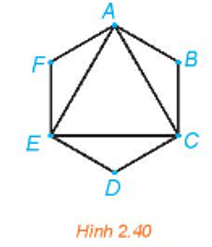
Bài 2.26 trang 51 Chuyên đề Toán 11: Tìm một chu trình Euler trong đồ thị trên Hình 2.40.
Lời giải:
Ta thấy đồ thị Hình 2.40 liên thông và mọi đỉnh của đồ thị này đều có bậc chẵn nên theo định lí Euler thì đồ thị này có một chu trình Euler.
Một chu trình Euler trong đồ thị trên Hình 2.40 là ABCDEFAECA.
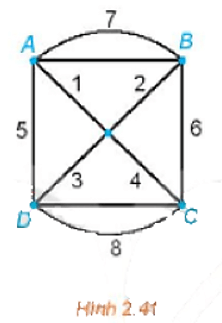
Lời giải:
Vì đồ thị Hình 2.41 là liên thông và các đỉnh đều có bậc chẵn (ở đây đều là bậc 4) nên đồ thị có chu trình Euler.
Một chu trình Euler xuất phát từ đỉnh A là ABCDABDCA và tổng độ dài của nó là
7 + 6 + 8 + 5 + 7 + 2 + 3 + 8 + 4 + 1 = 51.
Vậy một chu trình cần tìm là ABCDABDCA và có độ dài là 51.
Lời giải:
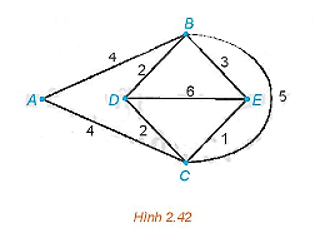
Đồ thị Hình 2.42 chỉ có hai đỉnh bậc lẻ là D và E nên ta có thể tìm được một đường đi Euler từ D đến E (đường đi này đi qua mỗi cạnh đúng một lần).
Một đường đi Euler từ D đến E là DBACDEBCE và tổng độ dài của nó là
2 + 4 + 4 + 2 + 6 + 3 + 5 + 1 = 27.
Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ E đến D theo thuật toán gắn nhãn vĩnh viễn.
Đường đi ngắn nhất từ E đến D là ECD và có độ dài là 1 + 2 = 3.
Vậy một chu trình cần tìm là DBACDEBCECD và có độ dài là 27 + 3 = 30.
Xem thêm các bài giải Chuyên đề học tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Bài 9: Đường đi Euler và đường đi Hamilton
Bài 10: Bài toán tìm đường tối ưu trong một vài trường hợp đơn giản