Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:

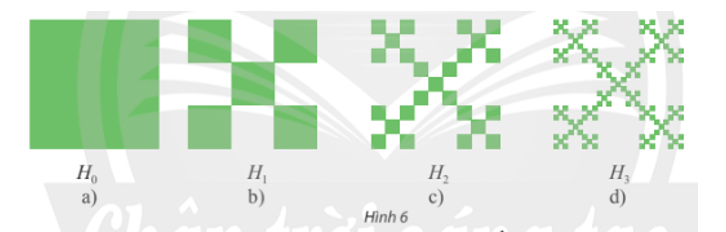
a) Bắt đầu một hình vuông H­₀ cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông H₀ thành chín hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình H₁ (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của H₁ thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình H₂ (xem Hình 6c). Tiếp tục quá trình này ta nhận được một dãy hình H_n(n = 1, 2, 3, ...).

a) Diện tích S_n của H_n là  $S_n=5^n.{\left(\frac{1}{3}\right)}^n.{\left(\frac{1}{3}\right)}^n=5^n.{\left(\frac{1}{3}\right)}^{2n}={\left(\frac{5}{9}\right)}^n$

Khi đó  ${\text{limS}}_n=\lim {\left(\frac{5}{9}\right)}^n=0$.