Vẽ đồ thị các hàm số sau: a) f(x) = x^2 khi x <= 2 và = ( x + 2 ) khi x > 2

Bài 2 trang 45 SBT Toán 10 Tập 1: Vẽ đồ thị các hàm số sau:

a) $f\left(x\right)=\left\{\begin{array}{l}{x}^{2}khix\le 2\\ x+2khix>2;\end{array}\right.$

b) f(x) = |x + 3| – 2. 

Trả lời

a) + Vẽ đồ thị hàm số g(x) = x² và giữ lại phần đồ thị ứng với x ≤ 2:

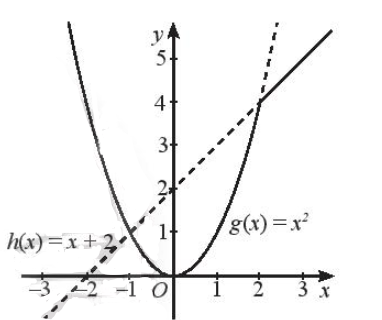
Đồ thị hàm số g(x) = x² là một parabol có đỉnh là gốc tọa độ O, trục đối xứng là trục Oy, đồ thị có bề lõm hướng lên trên, đi qua các điểm (1; 1), (– 1; 1), (2; 4), (– 2; 4).

Ta giữ lại phần đồ thị nằm bên trái đường thẳng x = 2:

+ Vẽ đồ thị hàm số h(x) = x + 2 và giữ lại phần đồ thị ứng với x > 2.

Đồ thị hàm số h(x) = x + 2 là một đường thẳng đi qua hai điểm (0; 2) và (– 2; 0).

Ta giữ lại phần đường thẳng nằm bên phải đường thẳng x = 2.

Ta được đồ thị cần vẽ như hình sau:

b) Với x + 3 ≥ 0 ⇔ x ≥ – 3, ta có: |x + 3| – 2 = x + 3 – 2 = x + 1.

Với x + 3 < 0 ⇔ x < – 3, ta có: |x + 3| – 2 = – (x + 3) – 2 = – x – 3 – 2 = – x – 5.

Khi đó ta có: $f\left(x\right)=\left\{\begin{array}{l}x+1khix\ge -3\\ -x-5khix<-3\end{array}\right.$.

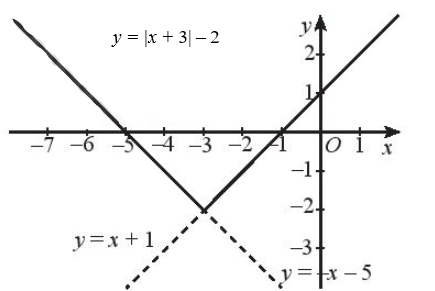
Ta vẽ đồ thị hàm số g(x) = x + 1 và giữ lại phần đồ thị ứng với x ≥ – 3: Đồ thị hàm số g(x) = x + 1 là đường thẳng đi qua hai điểm (0; 1) và (– 1; 0).

Ta vẽ đồ thị hàm số h(x) = – x – 5 và giữ lại phần đồ thị ứng với x < – 3: Đồ thị hàm số h(x) = – x – 5 là đường thẳng đi qua hai điểm (– 5; 0) và (– 3; – 2).

Ta được đồ thị của hàm số cần vẽ như hình sau:

Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của  góc từ 0° đến 180°