Vẽ ba đoạn thẳng AB, MN và PQ cùng có trung điểm I
Bài 5 trang 104 sách bài tập Toán lớp 6 Tập 2: Vẽ ba đoạn thẳng AB, MN và PQ cùng có trung điểm I.
Ba đoạn thẳng AB, MN và PQ cùng có trung điểm I nên:
IA = IB = AB : 2;
IM = IN = MN : 2;
IP = IQ = PQ : 2.
Ta có thể vẽ hình theo hai cách sau:
Cách 1: Tất cả các điểm đều nằm trên một đường thẳng hay cả ba đoạn thẳng trên một đường thẳng.
Ba đoạn thẳng AB, MN và PQ cùng có trung điểm I nên độ dài của ba đoạn thẳng này khác nhau (vì nếu bằng nhau thì ba đoạn thẳng này trùng nhau).
Chẳng hạn: AB > PQ > MN.
- Vẽ một đường thẳng bất kỳ, lấy điểm I thuộc đường thẳng này.
- Ta lấy các điểm A, B, P, Q, M, N thuộc đường thẳng này sao cho IA = IB, IP = IQ, IM = IN.
Ta có ba đoạn thẳng AB, MN và PQ cùng có trung điểm I như hình vẽ:
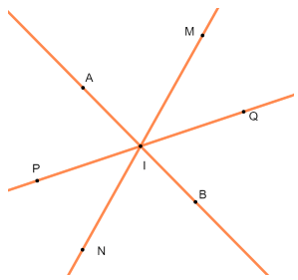
Cách 2: Tất cả các điểm không cùng nằm trên một đường thẳng hay ba đoạn thẳng không cùng nằm trên một đường thẳng.
Cách vẽ:
- Lấy điểm I bất kì.
- Qua I vẽ ba đường thẳng phân biệt (không có đường thẳng nào trùng nhau)
- Trên đường thẳng thứ nhất, lấy điểm A và B khác phía với điểm I sao cho IA = IB.
- Trên đường thẳng thứ hai, lấy điểm M và N khác phía với điểm I sao cho IM = IN.
- Trên đường thẳng thứ ba, lấy điểm P và Q khác phía so với điểm I sao cho IP = IQ.
Ta có ba đoạn thẳng AB, MN và PQ cùng có trung điểm I như hình vẽ:
Xem thêm các bài giải SBT Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Bài 7: Số đo góc. Các góc đặc biệt