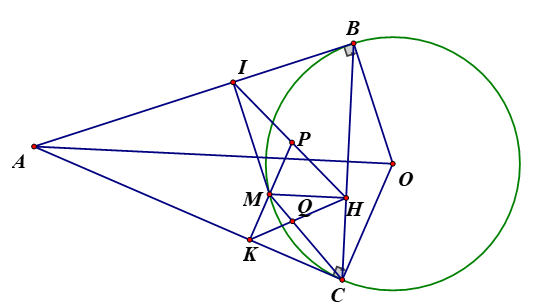
Từ điểm A ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB và AC( B,C là các tiếp điểm ). M là điểm bất kì trên cung nhỏ .
77
07/05/2024
Từ điểm A ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB và AC( B,C là các tiếp điểm ). M là điểm bất kì trên cung nhỏ .Kẻ là chân các đường vuông góc)
a) Chứng minh tứ giác nội tiếp.
b) Chứng minh
c) Gọi là giao điểm của IH và là giao điểm của KH và MC .
Chứng minh tứ giác nội tiếp.
Trả lời
a)Vì
VÌ
Ta có
Suy ra tứ giác nội tiếp(tứ giác có tổng hai góc đối diện bằng
b) Vì tứ giác Nội tiếp(c mt).suy ra
Trong đường tròn(O) cóGóc tạo bởi tía tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn một cung)(2).
Chứng minh tương tự câu a ta có tứ giác nội tiếp.
Từ và
Chứng minh tương tự ta có :
Từ (4) và
hay (đpcm)
c) Chứng minh:
Chứng minh:
Suy ra
Suy ra :(Tổng 3Goc trong tam giác MBC Hay
Suy ra tứ giác MPHD nội tiếp(tứ giác có tổng hai góc đối diện bằng