Câu hỏi:
03/04/2024 46Từ các chữ số 1,2,3,....,9 lập được bao nhiêu số có 3 chữ số đôi một khác nhau.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B
Lấy ra 3 chữ số từ 9 chữ số và sắp xếp 3 chữ số đó theo thứ tự, mỗi cách sắp xếp tạo nên 1 số có 3 chữ số khác nhau. Như vậy, có số cần tìm.
* Nhận xét: Mục đích bài toán là phân biệt hai khái niệm: Chỉnh hợp và tổ hợp. Học sinh có thể giải bài này bằng phương pháp nhân: 9.8.7, và so sánh với 4 đáp án. Hai chỉnh hợp khác nhau thì có thể khác nhau về phần tử hoặc khác nhau về thứ tự các phần tử. Hai tổ hợp khác nhau thì khác nhau về phần tử.
*Lý thuyết Chỉnh hợp
- Cho tập hợp A có n phần tử và cho số nguyên k, (1 k n). Khi lấy k phần tử của A và sắp xếp chúng theo một thứ tự, ta được một chỉnh hợp chập k của n phần tử của A (gọi tắt là một chỉnh hợp n chập k của A).
- Số các chỉnh hợp chập k của một tập hợp có n phần tử là: 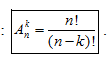
- Một số qui ước: ![]()
*Lý thuyết Tổ hợp
- Cho tập hợp A có n phần tử và cho số nguyên k, (1 k n). Mỗi tập hợp con của A có phần tử được gọi là một tổ hợp chập k của n phần tử của A.
- Số các chỉnh hợp chập k của một tập hợp có n phần tử là : 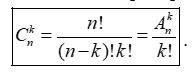
- Một số quy ước: ![]() với qui ước này ta có
với qui ước này ta có 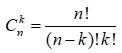 đúng với số nguyên dương k, thỏa 0 k n
đúng với số nguyên dương k, thỏa 0 k n
PT 14.1. Chọn B
TH1 ![]()
TH2: ![]() vì
vì ![]()
Như vậy, có ![]() số cần tìm
số cần tìm
PT 14.2.
Chọn C
Mỗi tập con có 3 phần tử thuộc tập {1,2,...,9} xác định duy nhất một số có 3 chữ số tăng dần từ trái qua phải (đảm bảo chữ số đầu tiên khác 0).
Mỗi tập con có 3 phần tử thuộc tập {0,1,2....,9} xác định duy nhất một số có 3 chữ số giảm dần từ trái qua phải.
Như vậy, có ![]() số cần tìm.
số cần tìm.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho một bảng ô vuông 3x3.
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng
Câu 2:
Nhãn mỗi chiếc ghế trong một hội trường gồm hai phần : phần đầu là một chữ cái ( trong bảng 24 chữ cái tiếng Việt ), phần thứ hai là một số nguyên dương nhỏ hơn 26. Hỏi có nhiều nhất bao nhiêu chiếc ghế được ghi nhãn khác nhau ?
Câu 3:
Cho tập hợp S = {1;2;3;4;5;6}. Gọi M là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau lấy từ S sao cho tổng của các chữ số hàng đơn vị , hàng chục và hàng trăm lớn hơn tổng các chữ số còn lại là 3. Tính tổng của các phần tử của tập hợp M.
Câu 4:
Một bộ đồ chơi ghép hình gồm các miếng nhựa. mỗi miếng nhựa được đặc trưng bởi ba yếu tố: màu sắc, hình dạng và kích cỡ. Biết rằng có 4 màu (xanh, đỏ, vàng, tím), có 3 hình dạng (hình tròn, hình vuông, hình tam giác) và 2 kích cỡ (to, nhỏ). Hộp đồ chơi đó có số miếng nhựa nhiều nhất là:
Câu 5:
Với k và n là hai số nguyên dương tùy ý thỏa mãn k n, mệnh đề nào dưới đây là đúng?
Câu 6:
Gọi A là tập hợp tất cả các số có dạng với a, b, c . Số phần tử của tập hợp A là
Câu 8:
Có bao nhiêu cách xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế?
Câu 9:
Với k và n là các số nguyên dương tùy ý thỏa mãn k n, mệnh đề nào dưới đây sai?
Câu 10:
Kí hiệu: (với k; n là những số nguyên dương và k n) có ý nghĩa là
Câu 11:
Có bao nhiêu số tự nhiên có 4 chữ số được viết từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 sao cho số đó chia hết cho 15?
Câu 12:
Có bao nhiêu cách chọn ra một tổ trưởng và một tổ phó từ một tổ có 10 người? Biết khả năng được chọn của mỗi người trong tổ là như nhau.
Câu 13:
Với k và n là hai số nguyên dương tùy ý thỏa mãn k n, mệnh đề nào dưới đây đúng?
Câu 14:
Gọi S là tập hợp các số tự nhiên gồm bốn chữ số đôi một khác nhau được lấy từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên một số từ S. Tính xác suất P để được một số chia hết cho 11 và tổng bốn chữ số của nó cũng chia hết cho 11.
Câu 15:
Từ các số 0, 1, 3, 4, 5, 7 có thể lập được bao nhiêu số tự nhiên có sáu chữ số khác nhau?


