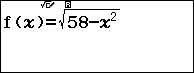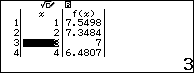Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm A và B dao động điều hòa cùng pha theo phương thẳng đứng tạo ra hai sóng kết hợp có bước sóng 4 cm. Khoảng cách
31
02/06/2024
Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm \[{\rm{A}}\]và \[{\rm{B}}\] dao động điều hòa cùng pha theo phương thẳng đứng tạo ra hai sóng kết hợp có bước sóng 4 cm. Khoảng cách giữa hai nguồn là AB = 30 cm. M là điểm ở mặt nước nằm ngoài hình tròn đường kính AB là cực đại giao thoa cùng pha với nguồn. H là trung điểm của AB. Độ dài ngắn nhất của đoạn MH gần nhất với giá trị nào sau đây?
A. 15,8 cm.
B. 15,2 cm.
C. 15,5 cm.
D. 16,2 cm.
Trả lời
Hướng dẫn
ĐK cực đại cùng pha nguồn \(\left\{ \begin{array}{l}MA = {k_1}\lambda \\MB = {k_2}\lambda \end{array} \right.\) với \({k_1}\), \({k_2}\) nguyên dương.
\[M{H^2} = \frac{{M{A^2} + M{B^2}}}{2} - \frac{{A{B^2}}}{4} = \frac{{{{\left( {4{k_1}} \right)}^2} + {{\left( {4{k_2}} \right)}^2}}}{2} - \frac{{{{30}^2}}}{4} > {15^2} \Rightarrow {k_1}^2 + {k_2}^2 > 56,25\]
Xét lần lượt \[{k_1}^2 + {k_2}^2 = 57 \to 58 \to 59...\]để tìm \[{\left( {{k_1}^2 + {k_2}^2} \right)_{\min }}\] có \({k_1}\), \({k_2}\) nguyên dương
Khi \[{k_1}^2 + {k_2}^2 = 58 \Rightarrow {k_2} = \sqrt {58 - k_1^2} \to \]TABLE START 1 STEP 1
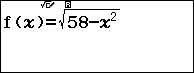
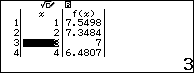(thỏa mãn)
Vậy \[M{H_{\min }} = \sqrt {\frac{{{4^2}.58}}{2} - \frac{{{{30}^2}}}{4}} \approx 15,46cm\]. Chọn C
