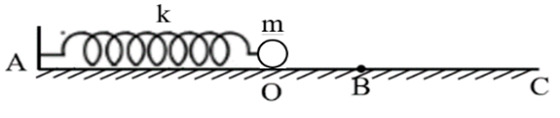
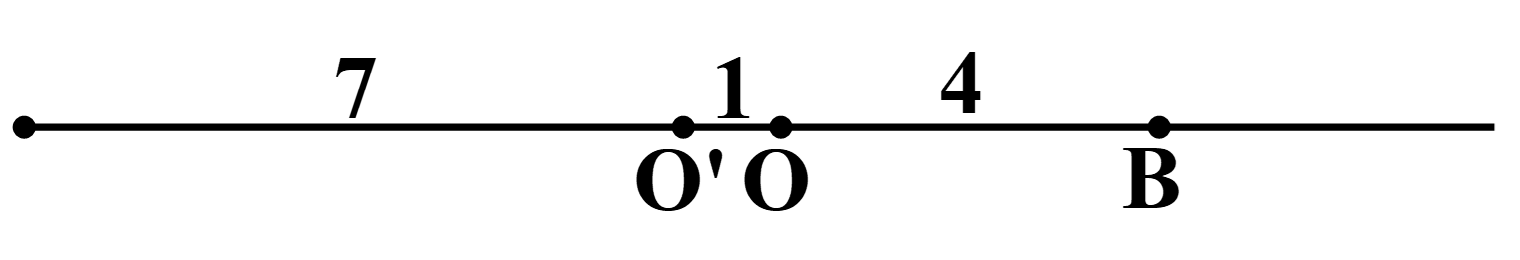Một con lắc lò xo gồm lò xo nhẹ có độ cứng k = 40 N/m, vật nhỏ có khối lượng m = 100 g đặt trên mặt bàn ngang như hình vẽ bên. Chiều dài tự nhiên của lò xo là OA = 30 cm. Mặt bàn có hai phần,
30
02/06/2024
Một con lắc lò xo gồm lò xo nhẹ có độ cứng k = 40 N/m, vật nhỏ có khối lượng m = 100 g đặt trên mặt bàn ngang như hình vẽ bên. Chiều dài tự nhiên của lò xo là OA = 30 cm. Mặt bàn có hai phần, phần nhẵn AB = 34 cm, phần nhám BC (đủ dài) có hệ số ma sát \[{\rm{\mu = 0}}{\rm{,4}}{\rm{.}}\] Lấy g = 10 m/s2. Ban đầu, giữ vật m sao cho lò xo bị nén 8 cm rồi thả nhẹ. Kể từ lúc thả, khoảng thời gian ngắn nhất để lò xo dãn cực đại gần nhất với giá trị nào sau đây?
A. 0,16 s.
B. 0,15 s.
C. 0,17 s.
D. 0,14 s.
Trả lời
Hướng dẫn
GĐ1: Dao động không ma sát đến B
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{40}}{{0,1}}} = 20\) (rad/s)
\(x = OB = AB - OA = 34 - 30 = 4cm\)
\(v = \omega \sqrt {{A^2} - {x^2}} = 20\sqrt {{8^2} - {4^2}} = 80\sqrt 3 cm/s\)
GĐ2: Dao động có ma sát với vtcb O’
\({F_{ms}} = \mu mg = 0,4.0,1.10 = 0,4\) (N)
\(O'O = \frac{{{F_{ms}}}}{k} = \frac{{0,4}}{{40}} = 0,01m = 1cm \to x' = 1 + 4 = 5cm\)
\(A' = \sqrt {x{'^2} + {{\left( {\frac{v}{\omega }} \right)}^2}} = \sqrt {{5^2} + {{\left( {\frac{{80\sqrt 3 }}{{20}}} \right)}^2}} = \sqrt {73} cm\)
\(t = \frac{{\arccos \frac{x}{{ - A}} + \arccos \frac{{x'}}{{A'}}}}{\omega } = \frac{{\arccos \frac{4}{{ - 8}} + \arccos \frac{5}{{\sqrt {73} }}}}{{20}} \approx 0,152s\). Chọn B
