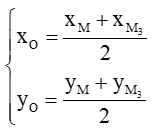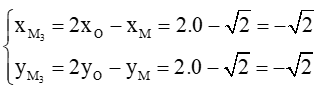Trong mặt phẳng tọa độ Oxy, tìm tọa độ của các điểm là ảnh của điểm  lần lượt qua các phép quay Q

Thực hành 1 trang 26 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, tìm tọa độ của các điểm là ảnh của điểm  lần lượt qua các phép quay Q_{(O, 45°)}, Q_{(O, 90°)}, Q_{(O, 180°)}, Q_{(O, 360°)}.

Trả lời

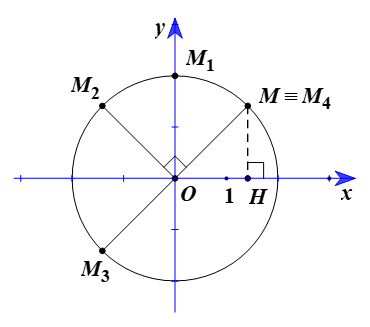
Ta có $\overrightarrow{\mathrm{OM}}=\left(\sqrt{2};\sqrt{2}\right)$. Suy ra OM = 2.

Vẽ đường tròn (C) tâm O bán kính OM.

⦁ Ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ qua phép quay Q_{(O, 45°)}:

Ta có Q_{(O, 45°)} biến điểm M khác O thành điểm M₁ sao cho OM₁ = OM = 2 và (OM, OM₁) = 45° nên $\widehat{{\mathrm{MOM}}_1}=45°$.

Kẻ MH ⊥ Ox tại H.

Tam giác OMH vuông tại H: $\cos \widehat{\mathrm{MOH}}=\frac{\mathrm{OH}}{\mathrm{OM}}=\frac{\sqrt{2}}{2}$.

Suy ra $\widehat{\mathrm{MOH}}=45°$.

Ta có $\widehat{{\mathrm{HOM}}_1}=\widehat{\mathrm{HOM}}+\widehat{{\mathrm{MOM}}_1}=45°+45°=90°$.

Suy ra M₁ ∈ Oy nên $x_{M_1}=0$.

Mà OM₁ = 2 (chứng minh trên) nên .

Vậy tọa độ M₁(0; 2).

⦁ Ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ qua phép quay Q_{(O, 90°)}:

Ta có Q_{(O, 90°)} biến điểm M khác O thành điểm M₂ sao cho OM₂ = OM = 2 và (OM, OM₂) = 90° nên $\widehat{{\mathrm{MOM}}_2}=90°$.

Suy ra tam giác MOM₂ vuông cân tại O.

Ta có $\widehat{M_1{\mathrm{OM}}_2}=\widehat{{\mathrm{MOM}}_2}-\widehat{{\mathrm{MOM}}_1}=90°-45°=45°$.

Suy ra $\widehat{{\mathrm{MOM}}_1}=\widehat{M_1{\mathrm{OM}}_2}=45°$.

Khi đó tam giác MOM₂ có OM₁ là đường phân giác.

Vì vậy OM₁ cũng là đường trung trực của tam giác MOM₂ hay Oy là đường trung trực của tam giác MOM₂.

Suy ra M₂ là ảnh của điểm M qua phép đối xứng trục Oy.

Do đó hai điểm $M\left(\sqrt{2};\sqrt{2}\right)$ và M₂ có cùng tung độ và có hoành độ đối nhau.

Vậy tọa độ $M_2\left(-\sqrt{2};\sqrt{2}\right)$.

⦁ Ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ qua phép quay Q_{(O, 180°)}:

Ta có Q_{(O, 180°)} biến điểm M khác O thành điểm M₃ sao cho OM₃ = OM = 2 và (OM, OM₃) = 180° nên $\widehat{{\mathrm{MOM}}_3}=180°$.

Suy ra O là trung điểm của MM₃.

Khi đó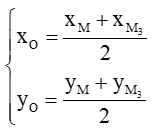 

Vì vậy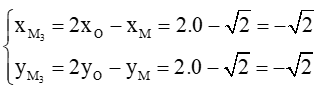 

Vậy tọa độ $M_3\left(-\sqrt{2};-\sqrt{2}\right)$.

⦁ Ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ qua phép quay Q_{(O, 360°)}:

Ta có Q_{(O, 360°)} biến điểm M khác O thành điểm M₄ sao cho OM₄ = OM = 2 và (OM, OM₄) = 360° nên $\widehat{{\mathrm{MOM}}_4}=360°$.

Tức là, M₄ ≡ M.

Vậy tọa độ $M_4\left(\sqrt{2};\sqrt{2}\right)$.

Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Phép đối xứng trục

Bài 4: Phép đối xứng tâm

Bài 5: Phép quay

Bài 6: Phép vị tự

Bài 7: Phép đồng dạng

Bài tập cuối chuyên đề 1