Bài 5 trang 29 Chuyên đề Toán 11: Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằm trên đoạn AB’ và nằm ngoài đoạn A’B. Gọi G và G’ lần lượt là trọng tâm của ∆OAA’ và ∆OBB’. Chứng minh rằng ∆OGG’ là tam giác vuông cân.
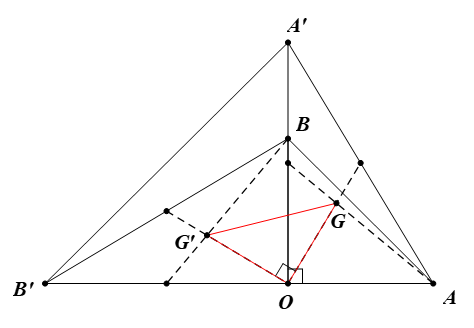
Do DOAB là tam giác vuông cân nên OA = OB và .
Do DOA’B’ là tam giác vuông cân nên OA’ = OB’ và .
Phép quay tâm O, góc quay 90° biến:
⦁ Điểm O thành điểm O;
⦁ Điểm A thành điểm B;
⦁ Điểm A’ thành điểm B’.
Do đó ảnh của ∆OAA’ qua phép quay tâm O, góc quay 90° là ∆OBB’.
Mà G, G’ lần lượt là trọng tâm của ∆OAA’ và ∆OBB’.
Vì vậy ảnh của G qua phép quay tâm O, góc quay 90° là G’.
Suy ra OG = OG’ và .
DOGG’ có OG = OG’ và nên là tam giác vuông cân tại O.
Vậy ∆OGG’ vuông cân tại O.
Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác: