Trong mặt phẳng tọa độ Oxy, cho A(2; 1), B(‒2; 5) và C(‒5; 2). Tìm tọa độ của các vectơ

Bài 4.35 trang 72 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho A(2; 1), B(‒2; 5) và C(‒5; 2).

a) Tìm tọa độ của các vectơ $\overrightarrow{BA}$ và $\overrightarrow{BC}.$

b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.

Trả lời

a) Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có: $\overrightarrow{BA}=\left(4;-4\right)$ và $\overrightarrow{BC}=\left(-3;-3\right).$

b) Ta có: 

$\overrightarrow{BA}.\overrightarrow{BC}=4.\left(-3\right)+\left(-4\right).\left(-3\right)=-12+12=0$

$\Rightarrow \overrightarrow{BA}\perp \overrightarrow{BC}$

$\Rightarrow BA\perp BC$

$\Rightarrow \Delta ABC$ vuông tại B.

Do $\overrightarrow{BA}=\left(4;-4\right)\Rightarrow BA=\sqrt{4^2+{\left(-4\right)}^2}=4\sqrt{2}$;

$\overrightarrow{BC}=\left(-3;-3\right)\Rightarrow BC=\sqrt{{\left(-3\right)}^2+{\left(-3\right)}^2}=3\sqrt{2}$.

Với A(2; 1) và C(‒5; 2) ta có:

$\overrightarrow{AC}=\left(-7;1\right)\Rightarrow AC=\sqrt{{\left(-7\right)}^2+1^2}=\sqrt{50}=5\sqrt{2}$ 

Diện tích tam giác vuông ABC là:

$S_{\Delta ABC}=\frac{1}{2}.AB.BC=\frac{1}{2}.4\sqrt{2}.3\sqrt{2}=12$ (đơn vị diện tích)

Chu vi tam giác ABC là:

AB + BC + AC = $4\sqrt{2}+3\sqrt{2}+5\sqrt{2}=12\sqrt{2}$ (đơn vị độ dài)

c)  Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có tọa độ trọng tâm G của tam giác ABC là:

$\left\{\begin{array}{l}{x}_G=\frac{2+\left(-2\right)+\left(-5\right)}{3}=\frac{-5}{3}\\ y_G=\frac{1+5+2}{3}=\frac{8}{3}\end{array}\right.\Rightarrow G\left(\frac{-5}{3};\frac{8}{3}\right)$

Vậy tọa độ trọng tâm của tam giác ABC là: $G\left(\frac{-5}{3};\frac{8}{3}\right).$

d)

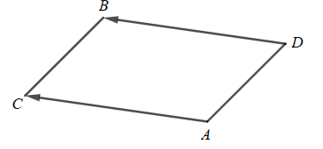
Để tứ giác BCAD là hình bình hành thì $\overrightarrow{AC}=\overrightarrow{DB}$

Giả sử D(x; y) là điểm cần tìm.

Với A(2; 1), B(‒2; 5) và C(‒5; 2) ta có: $\overrightarrow{AC}=\left(-7;1\right)$ và $\overrightarrow{DB}=\left(-2-x;5-y\right)$ 

Do đó $\overrightarrow{AC}=\overrightarrow{DB}$

$\iff \left\{\begin{array}{l}-2-x=-7\\ 5-y=1\end{array}\right.\iff \left\{\begin{array}{l}x=5\\ y=4\end{array}\right.\Rightarrow D\left(5;4\right)$.

Vậy với D(5;4) thì tứ giác BCAD là một hình bình hành. 

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

Bài 13: Các số đặc trưng đo xu thế trung tâm

Bài 14: Các số đặc trưng. Đo độ phân tán