Trong không gian Oxyz, cho hình lăng trụ tam giác đều ABC.A'B'C' có $A^{\text{'}}\left(\sqrt{3};-1;1\right),$  hai đỉnh B, C thuộc trục Oz và $A{A}^{\text{'}}=1$  (C không trùng với O). Biết vectơ $\overrightarrow{u}=(a;b;2)$  (với $a,b\in ℝ$) là một vectơ chỉ phương của đường thẳng A'C. Tính  $T=a^2+b^2.$

A.  $T=5.$

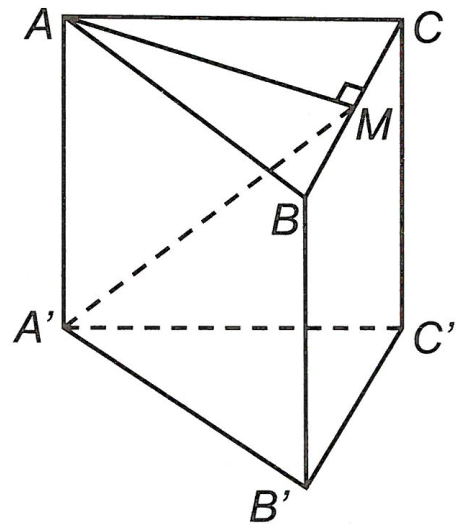
Lấy M là trung điểm BC.

Khi đó ta có $\left\{\begin{array}{l}AM\perp BC\\ A{A}^{\text{'}}\perp BC\end{array}\right.$  nên $BC\perp A^{\text{'}}M$  tại M;

suy ra M là hình chiếu của A' trên trục Oz

 $\Rightarrow M\left(0;0;1\right)vàA^{\text{'}}M=2.$

Mặt khác  $AM=\sqrt{A^{\text{'}}{M}^2-A{A^{\text{'}}}^2}=\sqrt{3}.$

Lại có DABC đều nên  $AM=\frac{\sqrt{3}}{2}BC=\sqrt{3}$

$\Rightarrow BC=2\Rightarrow MC=1.$

Gọi $C\left(0;0;c\right),c\ne 0$  suy ra  $MC=\left|c-1\right|.$

$MC=1\iff \left|c-1\right|=1\iff \left[\begin{array}{l}c=0\\ c=2\end{array}\right.$ ( loại $c=0$ )  $\Rightarrow C\left(0;0;2\right).$

$\overrightarrow{A^{\text{'}}C}=\left(-\sqrt{3};1;1\right)$là một vectơ chỉ phương của đường thẳng  A'C

Suy ra $\overrightarrow{u}=\left(-2\sqrt{3};2;2\right)$  cũng là một vectơ chỉ phương củaA'C .

Vậy $a=-2\sqrt{3};b=2.$  Suy ra  $T=a^2+b^2=16.$

Chọn B