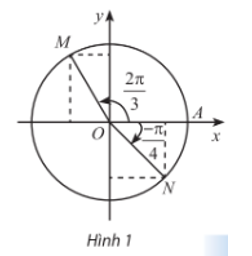
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác 2bi/3 và -bi/4 trên đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy.

Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác $\frac{2\mathrm{\pi }}{3}$ và $\frac{-\mathrm{\pi }}{4}$ trên đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy.

Trả lời

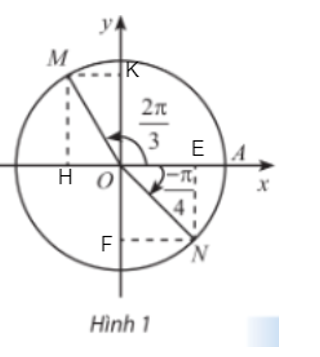
Gọi H, K lần lượt là hình chiếu của điểm M xuống trục Ox và Oy; gọi E, F lần lượt là hình chiếu của điểm N trên trục Ox và Oy.

Đặt $(OA,OM)=\alpha ,(OA,ON)=\beta$.

+) Xét tam giác MHO vuông tại H, có:

MH = $\sin \widehat{MOH}.MO=\sin \widehat{MOH}$

Ta có $\widehat{MOH}+\widehat{AOM}=180°$ nên $\sin \widehat{MOH}=\sin \widehat{AOM}$.

⇒ MH = $\sin \widehat{AOM}$ = sinα.

Mà MH = OK nên OK = sinα hay tung độ điểm M bằng sinα.

Ta lại có: OH = $\text{cos}\widehat{MOH}.MO=\text{cos}\widehat{MOH}$

_{Mà $\widehat{MOH}+\widehat{AOM}=180°$} nên $\text{cos}\widehat{MOH}=-\text{cos}\widehat{AOM}$

⇒ OH = $-\text{cos}\widehat{AOM}$ = – cosα do đó hoành độ của điểm M bằng cosα.

Vậy tọa độ điểm M là (cosα; sinα) = $\left(\text{cos}\frac{2\pi }{3};\sin \frac{2\pi }{3}\right)=\left(-\frac{1}{2};\frac{\sqrt{3}}{2}\right)$.

+) Xét tam giác ONE vuông tại E, có:

NE = $\sin \widehat{NOE}.ON=\sin \widehat{NOE}$

Mà $\widehat{NOE}=-\beta$

⇒ NE = – sinβ.

Mà NE = OF nên OF = – sinβ do đó tung độ điểm N bằng sinβ.

Ta lại có: OE = $\text{cos}\widehat{NOE}.ON=\text{cos}\widehat{NOE}$

⇒ OE = cosβ nên hoành độ của điểm M bằng cosβ.

Vậy tọa độ điểm N là (cosβ; sinβ) = $\left(\text{cos}\left(-\frac{\pi }{4}\right);\sin \left(-\frac{\pi }{4}\right)\right)=\left(\frac{\sqrt{2}}{2};-\frac{\sqrt{2}}{2}\right)$