Câu hỏi:
26/01/2024 59
Trong các phương án sau, phương án nào chứa hình có hai tam giác vuông không bằng nhau?
Trong các phương án sau, phương án nào chứa hình có hai tam giác vuông không bằng nhau?
A.
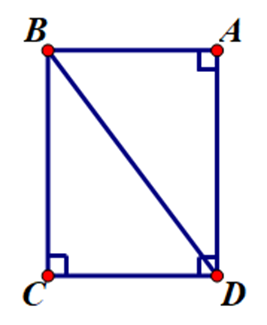
B.
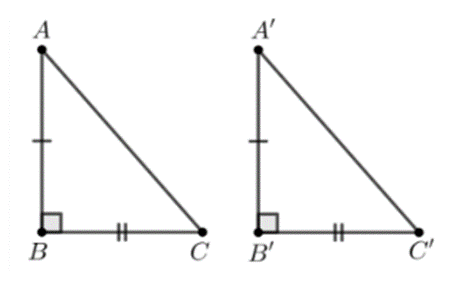
C.
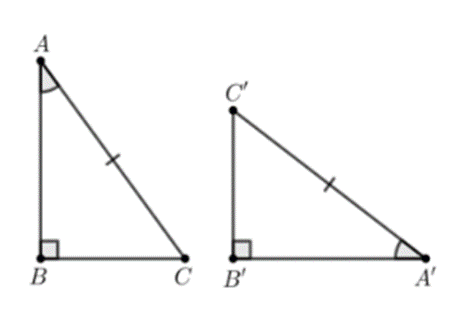
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Ta xét từng đáp án:
Đáp án A:
Xét ∆ABC và ∆A’B’C’, có:
\[\widehat {ABC} = \widehat {A'B'C'} = 90^\circ \],
AB = A’B’ (giả thiết),
BC = B’C’ (giả thiết).
Do đó ∆ABC = ∆A’B’C’ (hai cạnh góc vuông).
Vậy đáp án A đúng.
Đáp án B:
Xét ∆A’B’C’ và ∆ABC, có:
\[\widehat {A'B'C'} = \widehat {ABC} = 90^\circ \].
B’C’ = BC (giả thiết).
\[\widehat {A'C'B'} = \widehat {ACB}\] (giả thiết).
Do đó ∆A’B’C’ = ∆ABC (cạnh góc vuông – góc nhọn kề).
Vậy đáp án B đúng.
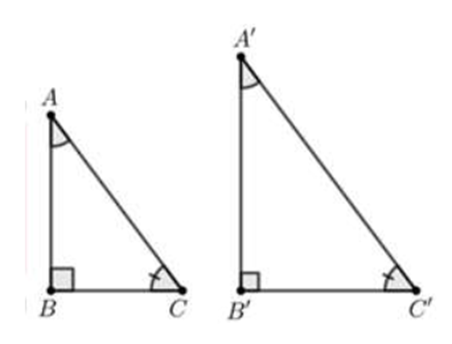
Đáp án C:
Xét ∆ABC và ∆A’B’C’, có:
\[\widehat {ABC} = \widehat {A'B'C'} = 90^\circ \].
AC = A’C’ (giả thiết).
\[\widehat {BAC} = \widehat {B'A'C'}\] (giả thiết).
Do đó ∆ABC = ∆A’B’C’ (cạnh huyền – góc nhọn).
Vậy đáp án C đúng.
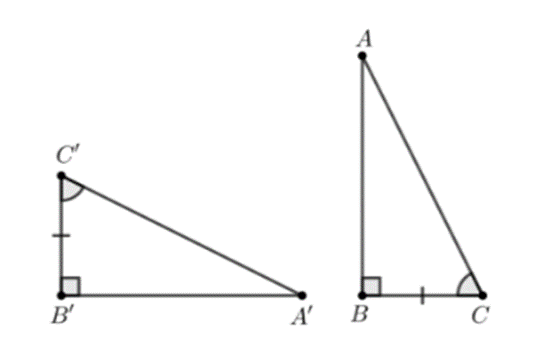
Đáp án D:
Xét ∆ABC và ∆A’B’C’, có các dữ kiện sau:
\[\widehat {ABC} = \widehat {A'B'C'} = 90^\circ \].
\[\widehat {BCA} = \widehat {B'C'A'}\] (giả thiết).
\[\widehat {BAC} = \widehat {B'A'C'}\] (giả thiết).
Tất cả các dữ kiện trên đều không phù hợp với cả bốn trường hợp bằng nhau của tam giác vuông.
Ta suy ra ∆ABC ≠ ∆A’B’C’.
Do đó hình vẽ đáp án D chứa hai tam giác không bằng nhau.
Vậy ta chọn đáp án D.
Đáp án đúng là: D
Ta xét từng đáp án:
Đáp án A:
Xét ∆ABC và ∆A’B’C’, có:
\[\widehat {ABC} = \widehat {A'B'C'} = 90^\circ \],
AB = A’B’ (giả thiết),
BC = B’C’ (giả thiết).
Do đó ∆ABC = ∆A’B’C’ (hai cạnh góc vuông).
Vậy đáp án A đúng.
Đáp án B:
Xét ∆A’B’C’ và ∆ABC, có:
\[\widehat {A'B'C'} = \widehat {ABC} = 90^\circ \].
B’C’ = BC (giả thiết).
\[\widehat {A'C'B'} = \widehat {ACB}\] (giả thiết).
Do đó ∆A’B’C’ = ∆ABC (cạnh góc vuông – góc nhọn kề).
Vậy đáp án B đúng.
Đáp án C:
Xét ∆ABC và ∆A’B’C’, có:
\[\widehat {ABC} = \widehat {A'B'C'} = 90^\circ \].
AC = A’C’ (giả thiết).
\[\widehat {BAC} = \widehat {B'A'C'}\] (giả thiết).
Do đó ∆ABC = ∆A’B’C’ (cạnh huyền – góc nhọn).
Vậy đáp án C đúng.
Đáp án D:
Xét ∆ABC và ∆A’B’C’, có các dữ kiện sau:
\[\widehat {ABC} = \widehat {A'B'C'} = 90^\circ \].
\[\widehat {BCA} = \widehat {B'C'A'}\] (giả thiết).
\[\widehat {BAC} = \widehat {B'A'C'}\] (giả thiết).
Tất cả các dữ kiện trên đều không phù hợp với cả bốn trường hợp bằng nhau của tam giác vuông.
Ta suy ra ∆ABC ≠ ∆A’B’C’.
Do đó hình vẽ đáp án D chứa hai tam giác không bằng nhau.
Vậy ta chọn đáp án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC vuông tại A. Lấy E ∈ BC sao cho BA = BE. Từ E dựng đường thẳng vuông góc với BC, cắt AC tại D. Hỏi ∆ABD = ∆EBD theo trường hợp nào?
Cho ∆ABC vuông tại A. Lấy E ∈ BC sao cho BA = BE. Từ E dựng đường thẳng vuông góc với BC, cắt AC tại D. Hỏi ∆ABD = ∆EBD theo trường hợp nào?
Câu 2:
Cho \[\widehat {xOy}\] khác góc bẹt. Trên tia phân giác Ot của \[\widehat {xOy}\] lấy điểm A. Gọi M là trung điểm OA. Đường thẳng qua M vuông góc với OA cắt Ox, Oy theo thứ tự tại B, C. Cho các khẳng định sau:
(I). “∆OBM = ∆OCM theo trường hợp cạnh góc vuông – góc nhọn kề”.
(II). “∆OBM = ∆ABM theo trường hợp hai cạnh góc vuông.”
Chọn câu trả lời đúng.
Cho \[\widehat {xOy}\] khác góc bẹt. Trên tia phân giác Ot của \[\widehat {xOy}\] lấy điểm A. Gọi M là trung điểm OA. Đường thẳng qua M vuông góc với OA cắt Ox, Oy theo thứ tự tại B, C. Cho các khẳng định sau:
(I). “∆OBM = ∆OCM theo trường hợp cạnh góc vuông – góc nhọn kề”.
(II). “∆OBM = ∆ABM theo trường hợp hai cạnh góc vuông.”
Chọn câu trả lời đúng.
Câu 3:
Cho ∆FDE và ∆PQR có: \[\widehat E = \widehat R = 90^\circ \], DF = QP, \[\widehat D = \widehat P = 30^\circ \]. Phát biểu nào sau đây đúng?
Cho ∆FDE và ∆PQR có: \[\widehat E = \widehat R = 90^\circ \], DF = QP, \[\widehat D = \widehat P = 30^\circ \]. Phát biểu nào sau đây đúng?
Câu 4:
Cho ∆MNP và ∆GHI có \[\widehat M = \widehat G = 90^\circ \] và NP = HI. Cần thêm điều kiện gì để ∆MNP = ∆GHI theo trường hợp cạnh huyền – góc nhọn?
Cho ∆MNP và ∆GHI có \[\widehat M = \widehat G = 90^\circ \] và NP = HI. Cần thêm điều kiện gì để ∆MNP = ∆GHI theo trường hợp cạnh huyền – góc nhọn?
Câu 5:
Cho tam giác ABC nhọn có AH ⊥ BC tại H. Trên tia đối của tia AB, lấy điểm D sao cho AD = AB. Kẻ DE ⊥ AH tại E. Hỏi ∆AHB = ∆AED theo trường hợp nào?
Cho tam giác ABC nhọn có AH ⊥ BC tại H. Trên tia đối của tia AB, lấy điểm D sao cho AD = AB. Kẻ DE ⊥ AH tại E. Hỏi ∆AHB = ∆AED theo trường hợp nào?
Câu 7:
Cho ∆ABC và ∆DEF có BC = EF, . Cần thêm điều kiện gì để ∆ABC = ∆DEF theo trường hợp cạnh huyền – cạnh góc vuông?
Cho ∆ABC và ∆DEF có BC = EF, . Cần thêm điều kiện gì để ∆ABC = ∆DEF theo trường hợp cạnh huyền – cạnh góc vuông?
Câu 8:
Cho hình thang cân MNPQ như hình vẽ sau:
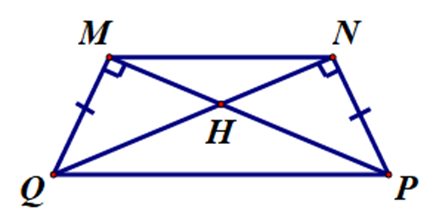
Trong hình bên có mấy cặp tam giác vuông bằng nhau?
Cho hình thang cân MNPQ như hình vẽ sau:

Trong hình bên có mấy cặp tam giác vuông bằng nhau?