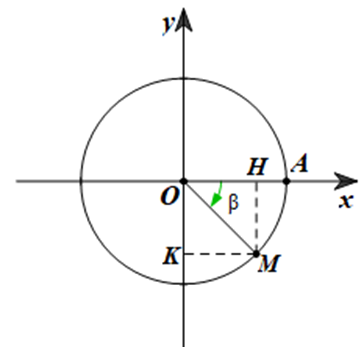
Lấy điểm M trên đường tròn lượng giác sao cho (OA, OM) = β = \( - \frac{\pi }{4} = - {\rm{45}}^\circ \) (hình vẽ).

Gọi H, K lần lượt là hình chiếu của điểm M trên các trục Ox, Oy.

Khi đó, ta có: \(\widehat {AOM} = {\rm{45}}^\circ \), suy ra \(\widehat {HOM} = \widehat {AOM} = {\rm{45}}^\circ \).

Theo hệ thức trong tam giác vuông HOM, ta có:

\(OH = OM.cos\widehat {HOM} = 1.c{\rm{os45}}^\circ = \frac{{\sqrt 2 }}{2}\);

\(OK = MH = OM.\sin \widehat {HOM} = 1.\sin {\rm{45}}^\circ = \frac{{\sqrt 2 }}{2}\).

Do đó \(M\left( {\frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 2 }}{2}} \right)\).

Vậy \[\sin \left( { - \frac{\pi }{4}} \right) = - \frac{{\sqrt 2 }}{2};cos\left( { - \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2};\]\(\tan \left( { - \frac{\pi }{4}} \right) = - 1;\cot \left( { - \frac{\pi }{4}} \right) = - 1\).