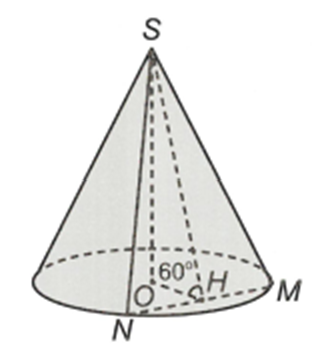
Thiết diện qua trục của một hình nón là tam giác vuông có cạnh góc vuông bằng 1. Mặt phẳng anpha qua đỉnh S của hình nón đó cắt đường tròn đáy tại M, N.
Thiết diện qua trục của một hình nón là tam giác vuông có cạnh góc vuông bằng 1. Mặt phẳng qua đỉnh S của hình nón đó cắt đường tròn đáy tại M, N. Tính diện tích tam giác SMN, biết góc giữa và đáy hình nón bằng 60o
A.
B.
C.
D.