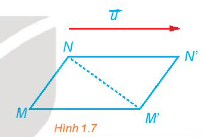
Phép tịnh tiến biến \({T_{\overrightarrow u }}\) biến M thành M', N thành N' (H.1.7).
a) Có nhận xét gì về \[\overrightarrow {MM'} + \overrightarrow {M'M} \] và \(\overrightarrow {M'N} + \overrightarrow {NN'} \).
b) Tìm mối quan hệ giữa hai vectơ và . \(\overrightarrow {MN} \)
Lời giải:
a) Phép tịnh tiến \({T_{\overrightarrow u }}\) biến điểm M thành M' thì \(\overrightarrow {MM'} = \overrightarrow u \) và biến N thành N' thì \(\overrightarrow {NN'} = \overrightarrow u \).
Ta có: \[\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow u + \overrightarrow {M'N} \] và \(\overrightarrow {M'N} + \overrightarrow {NN'} = \overrightarrow {M'N} + \overrightarrow u \).
Do đó, \[\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {M'N} + \overrightarrow {NN'} \].
b) Theo quy tắc ba điểm ta có: \[\overrightarrow {MN} = \overrightarrow {MM'} + \overrightarrow {M'N} \] và \[\overrightarrow {M'N'} = \overrightarrow {M'N} + \overrightarrow {NN'} \].
Mà theo câu a) ta có: \[\overrightarrow {MM'} + \overrightarrow {M'N} = \overrightarrow {M'N} + \overrightarrow {NN'} \].
Do đó, \(\overrightarrow {MN} = \overrightarrow {M'N'} \).