Một vật dao động điều hoà với tần số góc \(\omega = 5{\rm{rad}}/{\rm{s}}\). Khi \({\rm{t}} = 0\), vật đi qua vị trí có li độ \(x = - 2{\rm{\;cm}}\) và có vận tốc \(10{\rm{\;cm}}/{\rm{s}}\) hướng về vị trí biên gần hơn. Hãy viết phương trình dao động của vật.

Áp dụng công thức: \(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1 \Rightarrow A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{{\left( { - 2} \right)}^2} + \frac{{{{10}^2}}}{{{5^2}}}} = 2\sqrt 2 {\rm{\;cm}}{\rm{.\;}}\)

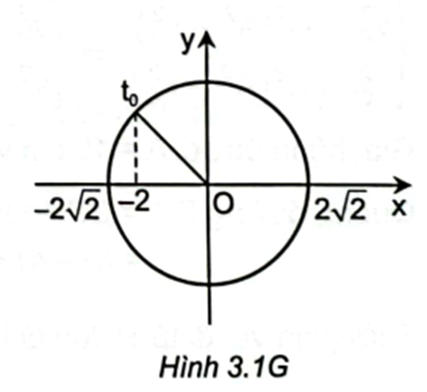
Theo đề bài khi \({\rm{t}} = 0\) thì: \(x = - 2{\rm{\;cm}} = - \frac{{A\sqrt 2 }}{2} < 0\) và có chiều hướng về vị trí biên gần nhất (Hình 3.1G) nên \(\varphi = \frac{{3\pi }}{4}\).

Phương trình dao động: \(x = 2\sqrt 2 {\rm{cos}}\left( {5t + \frac{{3\pi }}{4}} \right)\left( {{\rm{cm}}} \right).\)