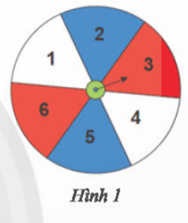
Một tấm bìa hình tròn được chia thành 6 phần bằng nhau như Hình 1.

Bạn Thủy quay mũi tên và quan sát xem khi dừng lại mũi tên chỉ vào ô số mấy. Thủy ghi lại kết quả sau 120 lần thí nghiệm ở bảng sau:

a) Tính xác suất thực nghiệm của biến cố "Mũi tên chỉ vào ô có màu trắng".

b) Theo em dự đoán, xác suất mũi tên chỉ vào mỗi ô có bằng nhau hay không?

c) Một người nhận định rằng xác suất mũi tên chỉ vào các ô có màu xanh bằng xác suất mũi tên chỉ vào các ô màu trắng và bằng xác suất mũi tên chỉ vào các ô có màu đỏ. Theo em, kết quả thực nghiệm của bạn Thủy có phù hợp với nhận định đó không?

Lời giải:

a) Xác suất thực nghiệm của biến cố "Mũi tên chỉ vào ô có màu trắng" là: 

\(\frac{{15 + 23}}{{120}} = \frac{{38}}{{120}} = \frac{{19}}{{60}}\).

b) Vì tấm bìa hình tròn được chia thành 6 phần bằng nhau nên xác suất mũi tên chỉ vào các ô là như nhau.

c) Xác suất thực nghiệm của biến cố "Mũi tên chỉ vào ô có màu xanh" là: 

\(\frac{{9 + 32}}{{120}} = \frac{{41}}{{120}}\).

Xác suất thực nghiệm của biến cố "Mũi tên chỉ vào ô có màu đỏ" là: 

\(\frac{{16 + 25}}{{120}} = \frac{{41}}{{120}} = 0,342\).

Theo kết quả thực nghiệm của bạn Thủy xác suất mũi tên chỉ vào các ô có màu xanh bằng xác suất mũi tên chỉ vào các ô màu đỏ và gần bằng xác suất mũi tên chỉ vào các ô có màu trắng \(\left( {\frac{{41}}{{120}} \ne \frac{{19}}{{60}}} \right)\).

Vì vậy, kết quả thực nghiệm của bạn Thủy có phù hợp với nhận định đó.