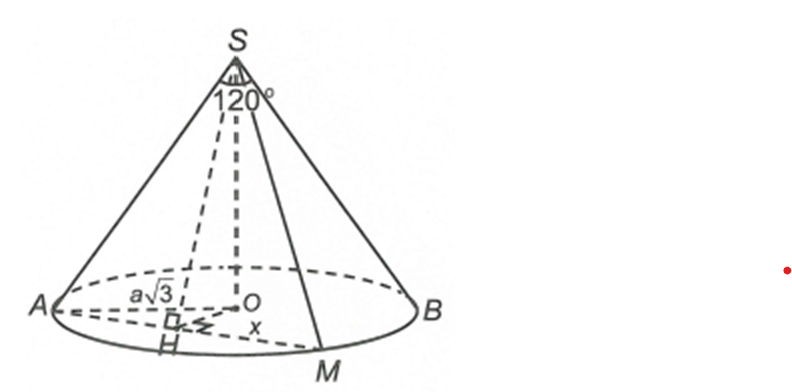
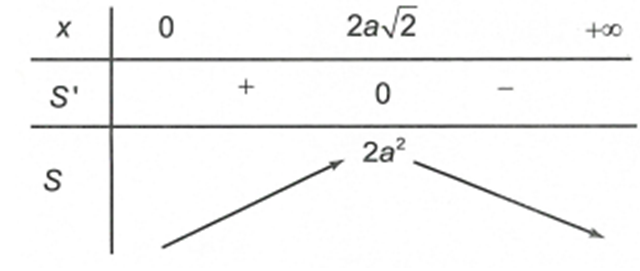
Một hình nón đỉnh S bán kính đáy R = a căn bậc hai 3, góc ở đỉnh là 120 độ. Mặt phẳng qua đỉnh hình nón cắt hình nón theo thiết diện là một tam giác
Một hình nón đỉnh S bán kính đáy , góc ở đỉnh là . Mặt phẳng qua đỉnh hình nón cắt hình nón theo thiết diện là một tam giác. Diện tích lớn nhất của tam giác đó bằng
A.
B.
C.
D.