Cách 1: Lớp 12
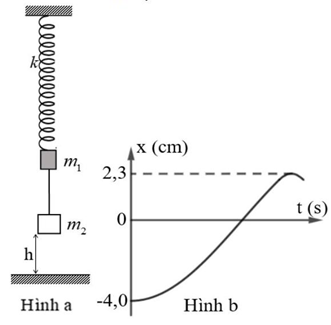
GĐ1: Cả 2 vật cùng dao động điều hòa đến khi m2 chạm đất
\(A = \Delta {l_0} = \frac{{\left( {{m_1} + {m_2}} \right)g}}{k} = \frac{{\left( {0,1 + 0,3} \right).10}}{{100}} = 0,04m = 4cm\)
\(\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} = \sqrt {\frac{{100}}{{0,1 + 0,3}}} = 5\sqrt {10} \) (rad/s)
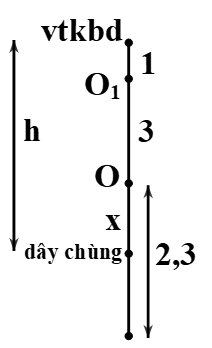
GĐ2: Dây chùng, m1 dao động với vị trí cân bằng mới O1 dãn
\(\Delta {l_1} = \frac{{{m_1}g}}{k} = \frac{{0,1.10}}{{100}} = 0,01m = 1cm\)
\({\omega _1} = \sqrt {\frac{k}{{{m_1}}}} = \sqrt {\frac{{100}}{{0,1}}} = 10\sqrt {10} \) (rad/s)
\(v = {v_1} \Rightarrow \omega \sqrt {{A^2} - {x^2}} = {\omega _1}\sqrt {A_1^2 - x_1^2} \Rightarrow 5\sqrt {10} .\sqrt {{4^2} - {x^2}} = 10\sqrt {10} .\sqrt {{{\left( {2,3 + 3} \right)}^2} - {{\left( {x + 3} \right)}^2}} \)
\( \Rightarrow x \approx 2cm \Rightarrow h = 4 + x = 6cm\). Chọn C
Cách 2: Lớp 10
Chọn mốc thế năng tại vị trí lò xo không biến dạng
Bảo toàn cơ năng cho hệ vật từ vị trí lò xo không biến dạng đến khi \({m_2}\) chạm đất (dây chùng)
\(0 = \frac{1}{2}k{h^2} + \frac{1}{2}\left( {{m_1} + {m_2}} \right){v^2} - \left( {{m_1} + {m_2}} \right)gh \Rightarrow \frac{1}{2}\left( {{m_1} + {m_2}} \right){v^2} = \left( {{m_1} + {m_2}} \right)gh - \frac{1}{2}k{h^2}\) (1)
Bảo toàn cơ năng cho vật m1 từ khi m2 chạm đất (dây chùng) đến khi m1 xuống vị trí thấp nhất
\(\frac{1}{2}k{h^2} + \frac{1}{2}{m_1}{v^2} - {m_1}gh = \frac{1}{2}k{s^2} - {m_1}gs \Rightarrow \frac{1}{2}{m_1}{v^2} = {m_1}g\left( {h - s} \right) + \frac{1}{2}k\left( {{s^2} - {h^2}} \right)\) (2)
Quãng đường vật m1 đi từ vị trí lò xo không biến dạng đến vị trí thấp nhất là
\(s = 4 + 2,3 = 6,3cm = 0,063m\)
Lấy \(\frac{{\left( 1 \right)}}{{\left( 2 \right)}} \Rightarrow \frac{{{m_1} + {m_2}}}{{{m_1}}} = \frac{{\left( {{m_1} + {m_2}} \right)gh - \frac{1}{2}k{h^2}}}{{{m_1}g\left( {h - s} \right) + \frac{1}{2}k\left( {{s^2} - {h^2}} \right)}}\)
\( \Rightarrow \frac{{0,1 + 0,3}}{{0,1}} = \frac{{\left( {0,1 + 0,3} \right).10.h - \frac{1}{2}.100.{h^2}}}{{0,1.10.\left( {h - 0,063} \right) + \frac{1}{2}.100.\left( {0,{{063}^2} - {h^2}} \right)}} \Rightarrow h \approx 0,06m = 6cm\). Chọn C