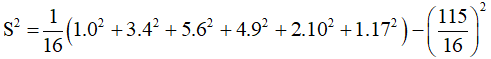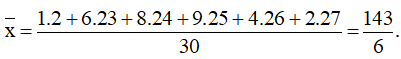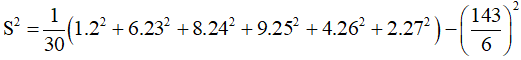Hãy tìm phương sai, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ (nếu có)

Bài 2 trang 129 SBT Toán 10 Tập 1: Hãy tìm phương sai, khoảng biến thiên, khoảng tứ phân vị và giá trị ngoại lệ (nếu có) của mỗi mẫu số liệu cho bởi bảng tần số sau:

a)

b)

Trả lời

a) Ta có: n = 1 + 3 + 5 + 4 + 2 + 1 = 16.

Số trung bình cộng:

$$\begin{gathered} \overline{x}=\frac{0.1+4.3+6.5+9.4+10.2+17.1}{16} \\ =\frac{115}{16}. \end{gathered}$$

Phương sai:

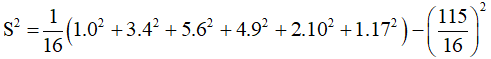
≈ 13,4.

Sắp xếp mẫu số liệu theo thứ tự không giảm:

0; 4; 4; 4; 6; 6; 6; 6; 6; 9; 9; 9; 9; 10; 10; 17

Khi đó, khoảng biến thiên R = 17 – 0 = 17.

Vì n = 16 là số chẵn nên ta có tứ phân vị thứ hai

Q₂ = (6 + 6) : 2 = 6.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 0; 4; 4; 4; 6; 6; 6; 6.

Vậy Q₁ = (4 + 6) : 2 = 5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 6; 9; 9; 9; 9; 10; 10; 17.

Vậy Q₃ = (9 + 9) : 2 = 9.

Khi đó khoảng tứ phân vị là ∆_Q = Q₃ − Q₁ = 9 – 5 = 4.

Giá trị ngoại lệ x thỏa mãn

x > Q₃ + 1,5∆_Q = 9 + 1,5.4 = 15

Hoặc x < Q₁ − 1,5∆_Q = 5 − 1,5.4 = −1.

Vậy đối chiếu mẫu số liệu suy ra giá trị ngoại lệ là 17.

b) Ta có: n = 1 + 6 + 8 + 9 + 4 + 2 = 30.

Số trung bình cộng:

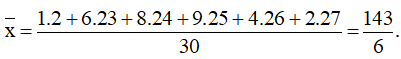
Phương sai:

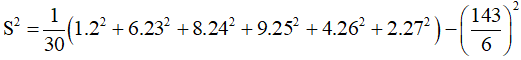
≈ 17,74.

Sắp xếp mẫu số liệu theo thứ tự không giảm:

2; 23; 23; 23; 23; 23; 23; 24; 24; 24; 24; 24; 24; 24; 24; 25; 25; 25; 25; 25; 25; 25; 25; 25; 26; 26; 26; 26; 27; 27

Khi đó, khoảng biến thiên R = 27 – 2 = 25.

Vì n = 30 là số chẵn nên ta có tứ phân vị thứ hai

Q₂ = (24 + 25) : 2 = 24,5.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 2; 23; 23; 23; 23; 23; 23; 24; 24; 24; 24; 24; 24; 24; 24.

Vậy Q₁ = 24.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 25; 25; 25; 25; 25; 25; 25; 25; 25; 26; 26; 26; 26; 27; 27.

Vậy Q₃ = 25.

Khi đó khoảng tứ phân vị là ∆_Q = Q₃ − Q₁ = 25 – 24 = 1.

Giá trị ngoại lệ x thỏa mãn

x > Q₃ + 1,5∆_Q = 25 + 1,5 = 26,5

Hoặc x < Q₁ − 1,5∆_Q = 24 − 1,5.1 = 22,5.

Vậy đối chiếu mẫu số liệu suy ra giá trị ngoại lệ là 2 và 27.

Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài tập cuối chương 6

Bài 1: Dấu của tam thức bậc hai

Bài 2: Giải bất phương trình bậc hai một ẩn