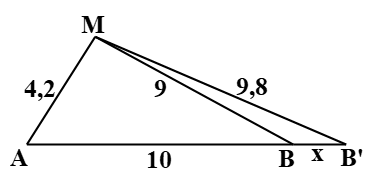
Hai nguồn phát sóng kết hợp A, B trên mặt nước cách nhau $10{\rm{\;cm}}$ dao động theo phương trình ${u_1} = {u_2} = 2{\rm{cos}}40\pi t\;\left( {{\rm{cm}}} \right)$. Xét điểm ${\rm{M}}$ trên mặt nước cách ${\rm{A}},{\rm{B}}$ sao cho ${\rm{MA}} = 4,2{\rm{\;cm}}$ và ${\rm{MB}} = 9{\rm{\;cm}}$. Coi biên độ sóng không đổi và tốc độ truyền sóng trên mặt nước là ${\rm{v}} = 32{\rm{\;cm}}/{\rm{s}}$. Giữ nguyên tần số $f$ và các vị trí $A,M$. Cân dịch chuyển nguồn $B$ xa nguồn $A$ (dọc theo phương $AB)$ một đoạn nhỏ nhất bao nhiêu để tại $M$ là một cực tiểu giao thoa?

D. $7,47{\rm{\;mm}}$

$\lambda = v.\frac{{2\pi }}{\omega } = 32.\frac{{2\pi }}{{40\pi }} = 1,6$(cm)

Ban đầu ${k_M} = \frac{{MB - MA}}{\lambda } = \frac{{9 - 4,2}}{{1,6}} = 3$

Lúc sau MB tăng thì ${k_M} = \frac{{MB' - 4,2}}{{1,6}} = 3,5 \Rightarrow MB' = 9,8$

$\cos \widehat {MBA} + \cos \widehat {MBB'} = 0 \Rightarrow \frac{{{{10}^2} + {9^2} - 4,{2^2}}}{{2.10.9}} + \frac{{{x^2} + {9^2} - 9,{8^2}}}{{2x.9}} = 0 \Rightarrow x \approx 0,874cm = 8,74mm$

Chọn A