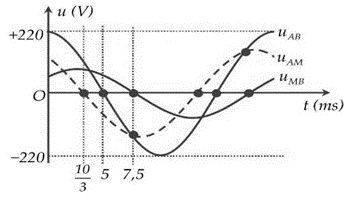
Cho mạch điện xoay chiều hai đầu \({\rm{AB}}\), gồm hai đoạn \({\rm{AM}}\) và \({\rm{MB}}\) mắc nối tiếp nhau. Điện áp tức thời giữa hai đầu \({\rm{AB}},{\rm{AM}},{\rm{MB}}\) tương ứng là \({{\rm{u}}_{{\rm{AB}}}},{{\rm{u}}_{{\rm{AM}}}},{{\rm{u}}_{{\rm{MB}}}}\) được biểu diễn bằng đồ thị hình bên theo thời gian \(t\). Biết cường độ dòng điện trong mạch có biểu thức \(i = \sqrt 2 {\rm{cos}}\omega t\;\left( A \right)\). Công suất tiêu thụ trên các đoạn mạch \({\rm{AM}}\) và \({\rm{MB}}\) lần lượt là

B. \(98,62{\rm{\;W}}\) và \(40,25{\rm{\;W}}\)

D. 98,62 W và \(56,94{\rm{\;W}}\)

\(\frac{T}{4} = {5.10^{ - 3}}s \Rightarrow T = 0,02s \to \omega = \frac{{2\pi }}{T} = 100\pi {\rm{ }}rad/s\)

\(\left\{ \begin{array}{l}{u_{AB}} = {U_{0AB}}\cos \left( {100\pi t} \right) = 220\cos \left( {100\pi t} \right)\\{u_{AM}} = {U_{0AM}}\cos \left[ {100\pi \left( {t - \frac{{10}}{3}{{.10}^{ - 3}}} \right) + \frac{\pi }{2}} \right] = {U_{0AM}}\cos \left( {100\pi t + \frac{\pi }{6}} \right)\end{array} \right.\)

Tại \(t = 7,{5.10^{ - 3}}s\) thì \({u_{AB}} = {u_{MB}} \Rightarrow 220\cos \frac{{3\pi }}{4} = {U_{0AM}}\cos \frac{{11\pi }}{{12}} \Rightarrow {U_{0AM}} \approx 161V\)

\({P_{AM}} = {U_{AM}}I\cos {\varphi _{AM}} = \frac{{161}}{{\sqrt 2 }}.1.\cos \frac{\pi }{6} \approx 98,62W\)

\({P_{AB}} = {U_{AB}}I\cos {\varphi _{AB}} = \frac{{220}}{{\sqrt 2 }}\) (W)

\({P_{MB}} = {P_{AB}} - {P_{AM}} = \frac{{220}}{{\sqrt 2 }} - 98,62 \approx 56,94W\). Chọn D

Note: Đường \({u_{MB}}\) trên đồ thị là không cần thiết