Câu hỏi:
03/04/2024 32Gọi S là tập hợp các số tự nhiên, mỗi số không có quá 3 chữ số và tổng các chữ số bằng 9. Lấy ngẫu nhiên một số từ 
. Tính xác suất để số lấy ra có chữ số hàng trăm là 4.
Trả lời:
Giải bởi Vietjack
Chọn A
- Bổ đề: Cho 
, ta có:
“Số nghiệm nguyên không âm của phương trình 
Thật vậy: Đặt 
Khi đó 
và 
Hiển nhiên số nghiệm nguyên không âm của (1) bằng số nghiệm nguyên dương của (2)
- Xếp m + n chữ số 1 thành một hàng: có 1 cách.
- Xếp n - 1 dấu gạch ngang "-" vào trong m + n -1 khoảng trống giữa các chữ số 1 (mỗi khoảng trống nhiều nhất một dấu gạch ngang) để chia dãy m + n chữ số 1 thành n phần (mỗi phần có ít nhất một chữ số 1): có cách.
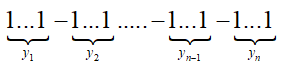
Mỗi phần được chia ra có tổng các chữ số 1 lần lượt là 
và cho ta một nghiệm nguyên dương của phương trình (2).
Do đó số nghiệm nguyên dương của phương trình (2) là 
Suy ra số nghiệm nguyên không âm của phương trình (1) là (đpcm)
Bây giờ ta sẽ áp dụng kết quả của bổ đề để giải bài toán đã cho:
- Tính số phần tử của tập S:
Gọi phần tử của S là vơí 
và a + b + c = 9 (*)
Theo bổ đề thì số nghiệm nguyên không âm của (*) là 
Vậy n(S) = 55
- Tính số các phần tử của S có chữ số hàng trăm bằng 4.
Khi đó a= 4 và b + c = 5 (**).
Theo bổ đề thì số nghiệm nguyên không âm của (**) là 
Vậy có tất cả 6phần tử của S có chữ số hàng trăm bằng 4.
- Xét phép thử: “Lấy ngẫu nhiên một số từ tập S” và biến cố A: “Số lấy ra có chữ số hàng trăm bằng 4”
Ta có 
Vậy xác suất của biến cố A là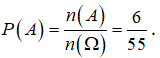 
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tổ 1 của lớp 10A có 10 học sinh gồm 6 nam và 4 nữ. Cần chọn ra 2 bạn trong tổ 1 để phân công trực nhật. Xác suất để chọn được 1 bạn nam và 1 bạn nữ là
Câu 2:
Một hộp có 10 quả cầu xanh, 5 quả cầu đỏ. Lấy ngẫu nhiên 5 quả từ hộp đó. Xác suất để được 5 quả có đủ hai màu là
Câu 3:
Một tổ học sinh có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn đều là nữ.
Câu 4:
Cho tập hợp A có 20 phần tử. Có bao nhiêu tập con của A khác rỗng và số phần tử là số chẵn?
Câu 5:
Một hộp đựng 7 viên bi đỏ đánh số từ 1 đến 7 và 6 viên bi xanh đánh số từ 1 đến 6. Hỏi có bao nhiêu cách chọn hai viên bi từ hộp đó sao cho chúng khác màu và khác số?
Câu 6:
Trên kệ sách có 10 cuốn sách Toán và 5 cuốn sách Văn. Người ta lấy ngẫu nhiên lần lượt 3 cuốn sách mà không để lại. Tính xác suất để được hai cuốn sách đầu là Toán, cuốn thứ ba là Văn.
Câu 7:
Cho phép thử là “gieo 10 đồng xu phân biệt” và xét sự xuất hiện mặt sấp và mặt ngửa của các đồng xu. Xác suất để có đúng một lần suất hiện mặt ngửa là
Câu 8:
Chọn ngẫu nhiên một số tự nhiên trong các số tự nhiên có bốn chữ số. Tính xác suất để số được chọn có ít nhất hai chữ số 8 đứng liền nhau.
Câu 9:
Xếp ngẫu nhiên 4 quyển sách Toán khác nhau và 4 quyển sách Hóa giống nhau vào một giá sách nằm ngang có 10 ô trống, mỗi quyển sách được xếp vào một ô. Xác suất để 4 quyển sách Toán xếp cạnh nhau và 4 quyển sách Hóa xếp cạnh nhau bằng
Câu 10:
Với các chữ “LẬP”, “HỌC”, “MAI”, “NGÀY”, “NGHIỆP”, “TẬP”, “VÌ”, mỗi chữ được viết lên một tấm bìa, sau đó người ta trải ra ngẫu nhiên. Xác suất để được dòng chữ “HỌC TẬP VÌ NGÀY MAI LẬP NGHIỆP” bằng:
Câu 11:
Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất để xuất hiện mặt chẵn chấm?
Câu 12:
Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4 quả cầu. Tính xác suất để trong 
quả cầu lấy được có đúng 4 quả cầu vàng.
Câu 14:
Xét một phép thử có không gian mẫu và A là một biến cố của phép thử đó. Phát biểu nào sau đây sai ?
Câu 15:
Một tổ có 5 học sinh nữ và 6 học sinh nam. Xếp ngẫu nhiên các học sinh trên thành hàng ngang để chụp ảnh. Tính xác suất để không có hai học sinh nữ nào đứng cạnh nhau.
