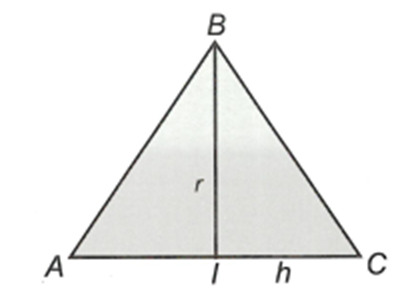
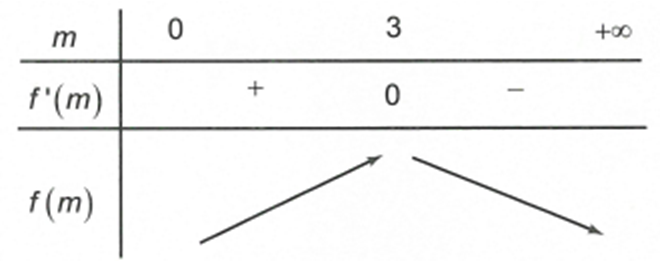
Giả sử đồ thị hàm số y = (m^2+1)x^4 - 2mx^2 + m^2 + 1 có 3 điểm cực trị là A, B, C mà xA < xB < xC. Khi quay tam giác ABC quanh cạnh AC ta được một khối tròn xoay.
Giả sử đồ thị hàm số có 3 điểm cực trị là A, B, C mà . Khi quay tam giác ABC quanh cạnh AC ta được một khối tròn xoay. Giá trị của m để thể tích của khối tròn xoay đó lớn nhất thuộc khoảng nào trong các khoảng dưới đây?
A. (4;6)
B. (2;4)
C. (-2;0)
D. (0;2)