Câu hỏi:

01/04/2024 63

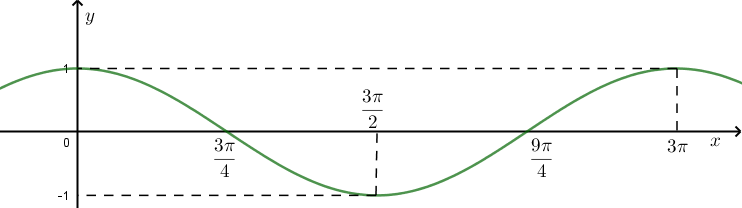
Đồ thị hàm số $y = \sin x$ được suy từ đồ thị $(C)$ của hàm số $y = \cos x + 1$ bằng cách:

A. Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2}$ và lên trên 1 đơn vị.

B. Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2}$ và lên trên 1 đơn vị.

C. Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2}$ và xuống dưới 1 đơn vị.

D. Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2}$ và xuống dưới 1 đơn vị.

Đáp án chính xác

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Ta có $y = \sin x = \cos (\frac{π}{2} - x) = \cos (x - \frac{π}{2}) .$

= Tịnh tiến đồ thị $y = \cos x + 1$ sang phải $\frac{π}{2}$ đơn vị ta được đồ thị hàm số $y = \cos (x - \frac{π}{2}) + 1.$

= Tiếp theo tịnh tiến đồ thị $y = \cos (x - \frac{π}{2}) + 1$ xuống dưới 1 đơn vị ta được đồ thị hàm số $y = \cos (x - \frac{π}{2}) .$ Chọn D

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm tập giá trị T của hàm số $y = \sin^{6} x + \cos^{6} x .$

Xem đáp án » 01/04/2024 230

Câu 2:

Hàm số $y = 5 + 4 \sin 2 x \cos 2 x$ có tất cả bao nhiêu giá trị nguyên?

Xem đáp án » 01/04/2024 140

Câu 3:

Hàm số $y = \cos^{2} x - \cos x$ có tất cả bao nhiêu giá trị nguyên?

Xem đáp án » 01/04/2024 138

Câu 4:

Hình bên là một phần đồ thị của hàm số nào sau đây?

Xem đáp án » 01/04/2024 131

Câu 5:

Tìm chu kì T của hàm số $y = \tan 3 x - \cos^{2} 2 x .$

Xem đáp án » 01/04/2024 131

Câu 6:

Tìm chu kì T của hàm số $y = \cos 3 x + \cos 5 x .$

Xem đáp án » 01/04/2024 118

Câu 7:

Gọi m,M lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = 8 \sin^{2} x + 3 \cos 2 x$ . Tính $P = 2 M - m^{2} .$

Xem đáp án » 01/04/2024 114

Câu 8:

Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x + \cos x$ . Tính $P = M - m .$

Xem đáp án » 01/04/2024 113

Câu 9:

Tập giá trị T của hàm số $y = \sin 2017 x - \cos 2017 x .$

Xem đáp án » 01/04/2024 113

Câu 10:

Hàm số $y = \tan x + \cot x + \frac{1}{\sin x} + \frac{1}{\cos x}$ không xác định trong khoảng nào trong các khoảng sau đây?

Xem đáp án » 01/04/2024 112

Câu 11:

Tìm tập xác định D của hàm số $y = \tan (\frac{π}{2} \cos x) .$

Xem đáp án » 01/04/2024 111

Câu 12:

Tìm chu kì T của hàm số $y = \cot \frac{x}{3} + \sin 2 x .$

Xem đáp án » 01/04/2024 110

Câu 13:

Cho hàm số $y = - 2 \sin (x + \frac{π}{3}) + 2$ . Mệnh đề nào sau đây là đúng?

Xem đáp án » 01/04/2024 110

Câu 14:

Tìm tập xác định của hàm số $y = \sqrt{1 - \cos x} + \cot x$ .

Xem đáp án » 01/04/2024 109

Câu 15:

Hàm số $y = \sin (x + \frac{π}{3}) - \sin x$ có tất cả bao nhiêu giá trị nguyên?

Xem đáp án » 01/04/2024 107

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

299 bài trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết

10 đề 3283 lượt thi Thi thử
100 câu trắc nghiệm Tổ hợp - Xác suất cơ bản

6 đề 2190 lượt thi Thi thử
Đề kiểm tra Giữa kì 2 Toán 11 có đáp án (Mới nhất)

24 đề 2078 lượt thi Thi thử
100 câu trắc nghiệm Đạo hàm nâng cao

5 đề 1944 lượt thi Thi thử
Bài tập chuyên đề toán 11 Bài 2: Giới hạn hàm số có đáp án

6 đề 1840 lượt thi Thi thử
100 câu trắc nghiệm Đạo hàm cơ bản

5 đề 1761 lượt thi Thi thử
100 câu trắc nghiệm Tổ hợp - Xác suất nâng cao

5 đề 1711 lượt thi Thi thử
160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án

5 đề 1621 lượt thi Thi thử
100 câu trắc nghiệm Hàm số lượng giác nâng cao

5 đề 1610 lượt thi Thi thử
100 câu trắc nghiệm Vecto trong không gian cơ bản

5 đề 1599 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

Câu hỏi:

A. Tịnh tiến (C)<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mi>C</mi></mfenced></math> qua trái một đoạn có độ dài là π2<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mi>π</mi><mn>2</mn></mfrac></math> và lên trên 1 đơn vị.

B. Tịnh tiến (C)<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mi>C</mi></mfenced></math> qua phải một đoạn có độ dài là π2<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mi>π</mi><mn>2</mn></mfrac></math> và lên trên 1 đơn vị.

C. Tịnh tiến (C)<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mi>C</mi></mfenced></math> qua trái một đoạn có độ dài là π2<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mi>π</mi><mn>2</mn></mfrac></math> và xuống dưới 1 đơn vị.

D. Tịnh tiến (C)<math xmlns="http://www.w3.org/1998/Math/MathML"><mfenced><mi>C</mi></mfenced></math> qua phải một đoạn có độ dài là π2<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mi>π</mi><mn>2</mn></mfrac></math> và xuống dưới 1 đơn vị.

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tìm tập giá trị T của hàm số y=sin6x+cos6x.<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><msup><mi>sin</mi><mn>6</mn></msup><mi>x</mi><mo>+</mo><msup><mi>cos</mi><mn>6</mn></msup><mi>x</mi><mo>.</mo></math>

Câu 2:

Hàm số y=5+4sin2xcos2x<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mn>5</mn><mo>+</mo><mn>4</mn><mi>sin</mi><mn>2</mn><mi>x</mi><mi>cos</mi><mn>2</mn><mi>x</mi></math> có tất cả bao nhiêu giá trị nguyên?

Câu 3:

Hàm số y=cos2x−cosx<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><msup><mi>cos</mi><mn>2</mn></msup><mi>x</mi><mo>−</mo><mi>cos</mi><mi>x</mi></math> có tất cả bao nhiêu giá trị nguyên?

Câu 4:

Hình bên là một phần đồ thị của hàm số nào sau đây?

Câu 5:

Tìm chu kì T của hàm số y=tan3x−cos22x.<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mi>tan</mi><mn>3</mn><mi>x</mi><mo>−</mo><msup><mi>cos</mi><mn>2</mn></msup><mn>2</mn><mi>x</mi><mo>.</mo></math>

Câu 6:

Tìm chu kì T của hàm số y=cos3x+cos5x.<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mi>cos</mi><mn>3</mn><mi>x</mi><mo>+</mo><mi>cos</mi><mn>5</mn><mi>x</mi><mo>.</mo></math>

Câu 7:

Câu 8:

Câu 9:

Tập giá trị T của hàm số y=sin2017x−cos2017x.<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mi>sin</mi><mn>2017</mn><mi>x</mi><mo>−</mo><mi>cos</mi><mn>2017</mn><mi>x</mi><mo>.</mo></math>

Câu 10:

Câu 11:

Tìm tập xác định D của hàm số y=tan(π2cosx).<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mi>tan</mi><mfenced><mrow><mfrac><mi>π</mi><mn>2</mn></mfrac><mi>cos</mi><mi>x</mi></mrow></mfenced><mo>.</mo></math>

Câu 12:

Tìm chu kì T của hàm số y=cotx3+sin2x.<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mi>cot</mi><mfrac><mi>x</mi><mn>3</mn></mfrac><mo>+</mo><mi>sin</mi><mn>2</mn><mi>x</mi><mo>.</mo></math>

Câu 13:

Cho hàm số y=−2sin(x+π3)+2<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mo>−</mo><mn>2</mn><mi>sin</mi><mfenced><mrow><mi>x</mi><mo>+</mo><mfrac><mi>π</mi><mn>3</mn></mfrac></mrow></mfenced><mo>+</mo><mn>2</mn></math> . Mệnh đề nào sau đây là đúng?

Câu 14:

Tìm tập xác định của hàm số y=√1−cosx+cotx<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><msqrt><mn>1</mn><mo>−</mo><mi>cos</mi><mi>x</mi></msqrt><mo>+</mo><mi>cot</mi><mi>x</mi></math> .

Câu 15:

Hàm số y=sin(x+π3)−sinx<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>y</mi><mo>=</mo><mi>sin</mi><mfenced><mrow><mi>x</mi><mo>+</mo><mfrac><mi>π</mi><mn>3</mn></mfrac></mrow></mfenced><mo>−</mo><mi>sin</mi><mi>x</mi></math> có tất cả bao nhiêu giá trị nguyên?

Đề thi liên quan

Câu hỏi mới nhất

A. Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2}$ và lên trên 1 đơn vị.

B. Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2}$ và lên trên 1 đơn vị.

C. Tịnh tiến $(C)$ qua trái một đoạn có độ dài là $\frac{π}{2}$ và xuống dưới 1 đơn vị.

D. Tịnh tiến $(C)$ qua phải một đoạn có độ dài là $\frac{π}{2}$ và xuống dưới 1 đơn vị.

Tìm tập giá trị T của hàm số $y = \sin^{6} x + \cos^{6} x .$

Hàm số $y = 5 + 4 \sin 2 x \cos 2 x$ có tất cả bao nhiêu giá trị nguyên?

Hàm số $y = \cos^{2} x - \cos x$ có tất cả bao nhiêu giá trị nguyên?

Tìm chu kì T của hàm số $y = \tan 3 x - \cos^{2} 2 x .$

Tìm chu kì T của hàm số $y = \cos 3 x + \cos 5 x .$

Tập giá trị T của hàm số $y = \sin 2017 x - \cos 2017 x .$

Tìm tập xác định D của hàm số $y = \tan (\frac{π}{2} \cos x) .$

Tìm chu kì T của hàm số $y = \cot \frac{x}{3} + \sin 2 x .$

Cho hàm số $y = - 2 \sin (x + \frac{π}{3}) + 2$ . Mệnh đề nào sau đây là đúng?

Tìm tập xác định của hàm số $y = \sqrt{1 - \cos x} + \cot x$ .

Hàm số $y = \sin (x + \frac{π}{3}) - \sin x$ có tất cả bao nhiêu giá trị nguyên?