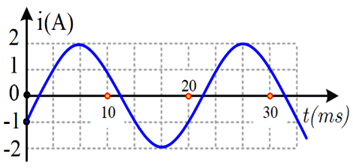
Đặt một điện áp xoay chiều vào hai đầu đoạn mạch gồm tụ điện có điện dung C = 36,75 μF mắc nối tiếp với điện trở có \(R = 50\,\,\Omega \). Hình bên là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện i trong đoạn mạch theo thời gian t. Biểu thức điện áp giữa hai đầu đoạn mạch theo thời gian t (t tính bằng s) là

B. \(u = 200\cos \left( {120\pi t + \frac{\pi }{3}} \right)\,V\).

D. \(u = 200\cos \left( {100\pi t + \pi } \right)\,V\).

Chọn D. \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{{{20.10}^{ - 3}}}} = 100\pi \;ra{\rm{d}}/s\).

\[{\user2{Z}_\user2{C}}\user2{ = }\frac{1}{{\user2{\omega C}}}\user2{ = }\frac{1}{{100\pi .36,{{75.10}^{ - 6}}}} \approx \user2{50}\sqrt 3 \Omega \]; \[Z = \sqrt {{R^2} + Z_C^2} = \sqrt {{{50}^2} + (50\sqrt 3 )_{}^2} = 100\Omega \].

\[{U_0} = {I_0}.Z = 2.100 = 200\]V;\[\user2{tan\varphi = }\frac{{\user2{ - }{\user2{Z}_\user2{C}}}}{\user2{R}}\user2{ = - }\frac{{\user2{50}\sqrt \user2{3} }}{{\user2{50}}}\user2{ = - }\sqrt \user2{3} \user2{ = > \varphi = - }\frac{\user2{\pi }}{\user2{3}}\];

Đồ thị cho ta: t =0 : i=-I₀/2 => \[{\user2{\varphi }_\user2{i}}\user2{ = - }\frac{{\user2{2\pi }}}{\user2{3}}\].

 \(u = {U_0}\cos \left( {100\pi t + {\varphi _i} + \varphi } \right)\,V = 200\cos \left( {100\pi t - \frac{{2\pi }}{3} + - \frac{\pi }{3}} \right)\, = 200\cos \left( {100\pi t - \pi } \right)\,\)V