Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
Ta có: n2+ n + 1 = (n . n + n) + 1 = n(n + 1) + 1
Vì n và n + 1 là hai số tự nhiên liên tiếp nên trong hai số n và n + 1, có một số là số chẵn.
TH1: n là số chẵn nên n ⁝ 2
Suy ra n(n + 1) ⁝ 2 (theo tính chất chia hết của một tích).
TH2: n + 1 là số chẵn nên (n + 1) ⁝ 2
Suy ra n(n + 1) ⁝ 2 (theo tính chất chia hết của một tích).
Do vậy trong mọi trường hợp thì n(n + 1) đều chia hết cho 2 nên nó là số chẵn, mà 1 là số lẻ nên n(n + 1) + 1 là số lẻ.
Vậy với mọi số tự nhiên n thì n2+ n + 1 là số lẻ.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
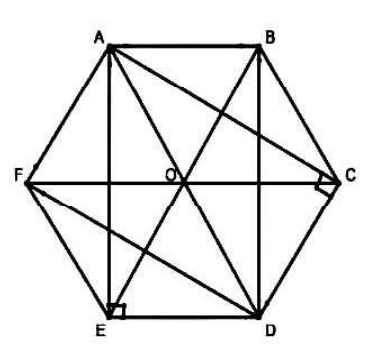
Một tòa tháp có đáy là hình lục giác đều ABCDEF.
a) Kể tên 2 hình tam giác đều, 2 hình thoi, 2 hình chữ nhật có trong hình bên.
b) Tính tổng diện tích hình chữ nhật ABDE và hình thoi AOEF theo đơn vị mét vuông. Cho AB = 90 cm; AE = 156 cm.
Câu 2:
Cô giáo chủ nhiệm lớp 6A muốn chia 240 cuốn vở, 72 bút, 168 tập giấy kiểm tra thành một số phần thưởng như nhau để thưởng cho học sinh có thành tích cao nhân dịp sơ kết đợt thi đua chào mừng ngày 20 - 11. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng? Khi đó, mỗi phần thưởng có bao nhiêu cuốn vở, bút, tập giấy kiểm tra?
Câu 3:
Thực hiện phép tính (hợp lý nếu có thể):
a) 38 + 53 + 62 + 57 + 22
b) 25.15 + 47.95 + 25.38 – 47.70
c) (23.93+ 92.45) : (92.15 – 2.92)
Câu 4:
Tìm số tự nhiên x, biết:
a) 2x + 4 = 23
b) 3x + 1 + 23 = 2.52.20220
c) 180 ⁝ x và 12 < x ≤ 20