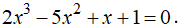Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chứng minh rằng phương trình sau có ít nhất hai nghiệm :
- Xét hàm số: là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
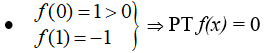
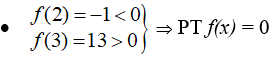
- Mà nên PT f(x) = 0 có ít nhất 2 nghiệm.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ diện ABCD có AB = AC và DB = DC. Khẳng định nào sau đây đúng?
Câu 4:
Giới hạn (nếu tồn tại và hữu hạn) nào sau đây dùng để định nghĩa đạo hàm của hàm số y = f(x) tại điểm ?
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, . Chứng minh rằng các mặt bên hình chóp là những tam giác vuông.
Câu 6:
Cho hàm số . Viết phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với
Câu 8:
Cho tứ diện ABCD với , CD=AD .Gọi là góc giữa AB và CD. Chọn khẳng định đúng?
Câu 10:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, . Tính góc giữa hai mặt phẳng (SBD) và (ABCD).
Câu 11:
Hàm số y = f(x) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
Câu 14:
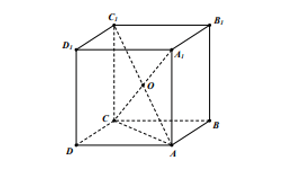
Cho hình lập phương . Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng: