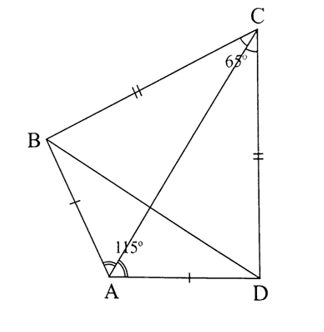
Cho tứ giác ABCD có AB = AD, CB = CD, góc C = 65 độ, góc A = 115 độ a) Chứng minh AC là đường trung trực của BD. b) Tính số đo góc B và góc D.
Cho tứ giác ABCD có AB = AD, CB = CD, ˆC=65°
a) Chứng minh AC là đường trung trực của BD.
b) Tính số đo góc B và góc D.