Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi H là chân đường vuông góc hạ từ O đến mặt phẳng (ABC). Chứng minh rằng:
a) BC (OAH);
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi H là chân đường vuông góc hạ từ O đến mặt phẳng (ABC). Chứng minh rằng:
a) BC (OAH);
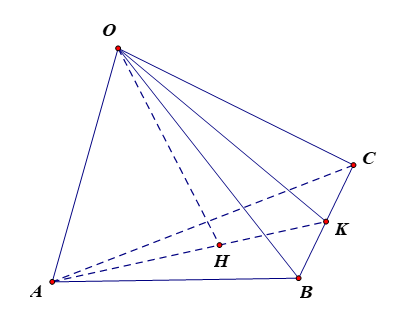
a) Vì OA OB, OA OC nên OA (OBC). Suy ra OA BC.
Mà OH (ABC) nên OH BC. Do đó BC (OAH).