Cho tứ diện ABCD có AB = AC và DB = DC. Chứng minh rằng AD vuông góc BC.
Cho tứ diện ABCD có AB = AC và DB = DC. Chứng minh rằng AD ⊥ BC.
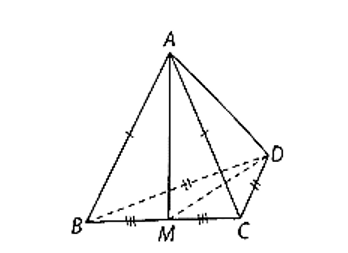
Gọi M là trung điểm của BC.
Xét tam giác ABC có AB = AC và AM là trung tuyến nên AM là đường cao.
Do đó AM ⊥ BC. (1)
Xét tam giác BCD có DC = DB và DM là trung tuyến nên DM là đường cao.
Do đó DM ⊥ BC. (2)
Từ (1) và (2) có: BC ⊥ (ADM). Suy ra BC ⊥ AD.