Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, BD. Điểm P thuộc cạnh AC sao cho PA = 2PC.

a) Xác định giao điểm E của đường thẳng MP với mặt phẳng (BCD).

b) Xác định giao điểm Q của đường thẳng CD với mặt phẳng (MNP).

c) Xác định giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).

d) Gọi I là giao điểm của MQ và NP, G là trọng tâm của tam giác ABD. Chứng minh rằng C, I, G thẳng hàng.

Lời giải

a)

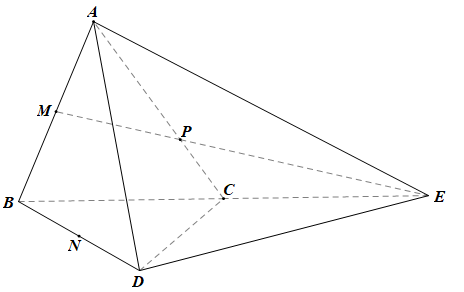
Trong mp(ABC), kéo dài MP cắt BC tại E. Nối AE, DE.

Ta có: MP ∩ BC = {E};

           BC ⊂ (BCD)

Do đó MP ∩ (BCD) = {E}.

b)

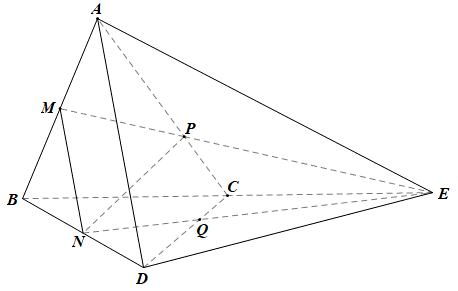
Nối NE, NE cắt CD tại Q.

Ta có: CD ∩ NE = {Q};

           NE ⊂ (MNP)

Do đó CD ∩ (MNP) = {Q}.

c)

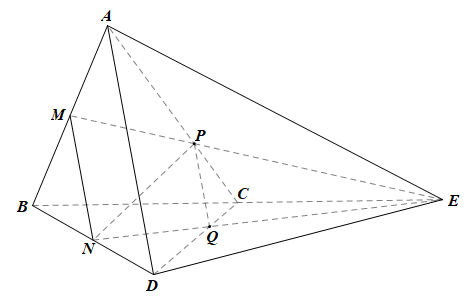
Ta có: P ∈ AC, mà AC ⊂ (ACD) nên P ∈ (ACD);

Mà P ∈ (MNP) nên P là giao điểm của (ACD) và (MNP).

Lại có Q ∈ CD và CD ⊂ (ACD) nên Q ∈ (ACD);

Mà Q ∈ (MNP) nên Q là giao điểm của (ACD) và (MNP).

Do đó PQ là giao tuyến của hai mặt phẳng (ACD) và (MNP).

d)

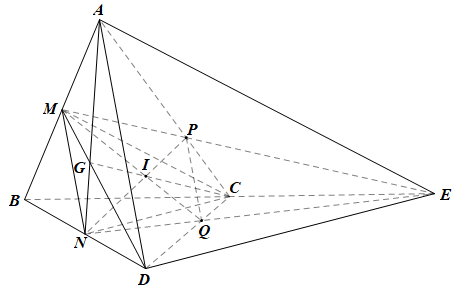
Do G là trọng tâm của tam giác ABD nên hai đường trung tuyến DM, AN của tam giác cùng đi qua G.

Ta có: G ∈ AN mà AN ⊂ (ANC) nên G ∈ (ANC);

           G ∈ DM mà DM ⊂ (MDC) nên G ∈ (MDC).

Do đó G là giao điểm của hai mặt phẳng (ANC) và (MDC).

Lại có: C ∈ (ANC) và C ∈ (MDC) nên C cũng là giao điểm của hai mặt phẳng (ANC) và (MDC).

Vậy GC là giao tuyến của hai mặt phẳng (ANC) và (MDC).

Mặt khác, I là giao điểm của MQ và NP nên I ∈ MQ và I ∈ NP.

Vì I ∈ MQ mà MQ ⊂ (MDC) nên I ∈ (MDC)

Vì I ∈ NP mà NP ⊂ (ANC) nên I ∈ (ANC)

Do đó giao tuyến GC của hai mặt phẳng (ANC) và (MDC) đi qua điểm I.

Vậy ba điểm C, I, G thẳng hàng.