Lời giải
a)
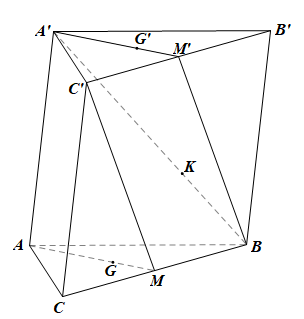
Trong mp(BCC’B’) có tứ giác BCC’B’ là hình bình hành nên BC // B’C’ và BC = B’C’.
Lại có M, N lần lượt là trung điểm của BC, B’C’ nên BM = C’M’ = \(\frac{1}{2}\)BC = \(\frac{1}{2}\)B’C’.
Tứ giác BMC’M’ có BM // C’M’ (do BC // B’C’) và BM = C’M’ nên BMC’M’ là hình bình hành
Do đó C’M // M’B, mà M’B ⊂ (A’BM’) nên C’M // (A’BM’).
b)
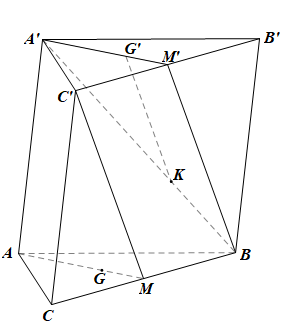
Trong mp(A’BM’), xét DA’BM’ có \(\frac{{A'G'}}{{A'M'}} = \frac{{A'K}}{{A'B}} = \frac{2}{3}\) nên G’K // M’B (theo định lí Thalès đảo)
Mà M’B ⊂ (BCC’B’) nên G’K // (BCC’B’).
c)
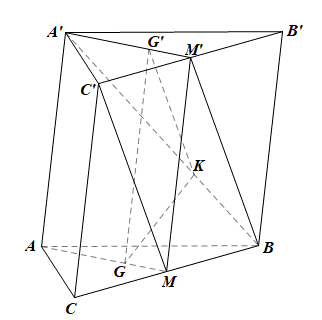
Trong mp(BCC’B’), tứ giác CMM’C’ có C’M’ // CM và C’M’ = CM = \(\frac{1}{2}\)BC = \(\frac{1}{2}\)B’C’
Do đó tứ giác CMM’C’ là hình bình hành nên M’M // C’C và M’M = C’C.
Mà A’A // C’C và A’A = C’C nên A’A // M’M và A’A = M’M.
Khi đó AMM’A’ là hình bình hành nên A’M’ // AM và A’M’ = AM.
Lại có \(\frac{{AG}}{{AM}} = \frac{{A'G'}}{{A'M'}} = \frac{2}{3}\) nên A’G’ = AG, do đó G’M’ = GM.
Xét tứ giác GMM’G’ có: G’M’ = GM (do A’M’ // AM) và G’M’ = GM.
Do đó GMM’G’ là hình bình hành nên G’G // M’M
Lại có M’M ⊂ (BCC’B’) nên G’G // (BCC’B’).
Ta có: G’K // (BCC’B’);
G’G // (BCC’B’);
G’K, G’G cắt nhau tại điểm G’ và cùng nằm trong (GG’K)
Do đó (GG’K) // ((BCC’B’).
d)
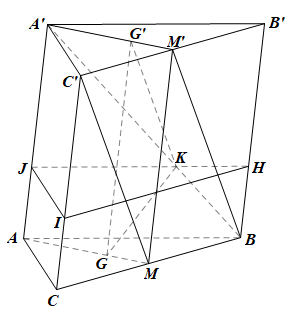
Trong mp(ABB’A’), vẽ đường thẳng qua K và song song với AB, A’B’; cắt A’A và B’B lần lượt tại J và H.
Trong mp (ACC’A”), vẽ đường thẳng qua J và song song với AC, A’C’; cắt C’C tại I.
Ta có: IJ // AC mà AC ⊂ (ABC) nên IJ // (ABC);
JK // AB mà AB ⊂ (ABC) nên JK // (ABC).
Lại có IJ và JK cắt nhau tại J và cùng nằm trong mp(IJK) nên (IJK) // (ABC).
Theo bài, mp(α) // (ABC) và đi qua K nên mp(α) chính là mp(IJK).
Khi đó CC’ cắt (α) tại I.
Ta có: (IJK) // (ABC) mà (ABC) // (A’B’C’) nên (A’B’C’), (IJK), (ABC) là ba mặt phẳng song song với nhau.
Xét hai cát tuyến C’C và A’B bất kì cắt ba mặt phẳng song song (A’B’C’), (IJK), (ABC) lần lượt tại các điểm C’, I, C và A’, K, B. Khi đó theo định lí Thalès trong không gian ta có: \(\frac{{C'I}}{{A'K}} = \frac{{IC}}{{KB}}\)
Suy ra \[\frac{{KB}}{{A'K}} = \frac{{IC}}{{C'I}}\]
Theo bài, \(\frac{{A'K}}{{A'B}} = \frac{2}{3}\) nên \(\frac{{A'B}}{{A'K}} = \frac{3}{2}\) do đó \(\frac{{A'B - A'K}}{{A'K}} = \frac{{3 - 2}}{2}\) hay \(\frac{{KB}}{{A'K}} = \frac{1}{2}\)
Vậy \[\frac{{IC}}{{IC'}} = \frac{{KB}}{{A'K}} = \frac{1}{2}\].




