Cho tứ diện ABCD, gọi M là N lần lượt là trung điểm của AC và BD. Biết $MN=a\sqrt{3}$; $AB=2\sqrt{2}a$ và CD = 2a. Chứng minh rằng đường thẳng AB vuông góc với đường thẳng CD.

Lấy K là trung điểm của BC.

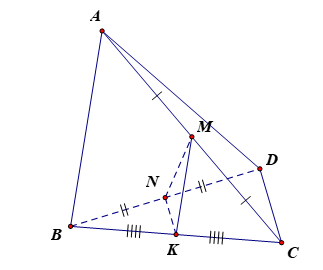
Xét tam giác BCD có N là trung điểm BD, K là trung điểm BC nên NK là đường trung bình. Do đó NK // CD và $NK=\frac{DC}{2}=a$.

Xét tam giác ABC có M là trung điểm AC, K là trung điểm BC nên MK là đường trung bình. Do đó MK // AB và $MK=\frac{AB}{2}=\sqrt{2}a$.

Có MN² = 3a² ; NK² + MK² = $a^2+{\left(\sqrt{2}a\right)}^2=3a^2$.

Do đó MN² = NK² + MK² nên tam giác MNK là tam giác vuông tại K hay NK ^ MK.

Lại có MK // AB, NK // CD nên (AB, CD) = (MK, NK) = 90° hay AB ^ CD.