Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ^ (BCD). Cho biết BC = $a\sqrt{2}$ , AB = $\frac{a}{\sqrt{3}}$ . Xác định và tính góc giữa hai mặt phẳng (ACD) và (BCD).

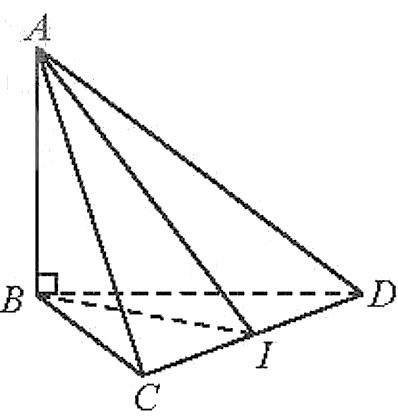
Gọi I là trung điểm của CD.

Ta có: CD ^ BI và CD ^ AB suy ra CD ^ AI.

Ta nhận thấy: CD là giao tuyến của 2 mặt phẳng (ACD) và (BCD);

Mà $\left\{\begin{array}{c}AI\perp CD,AI\subset \left(ACD\right)\\ BI\perp CD,BI\subset \left(BCD\right)\end{array}\right.$

Suy ra $\left(\right(ACD),(BCD\left)\right)=(AI,BI)=\widehat{AIB}.$

Tam giác BCD vuông cân tại B nên $BI=\frac{1}{2}CD=\frac{1}{2}.BC.\sqrt{2}=a.$

Xét tam giác ABI vuông tại B, ta có: $\tan \widehat{AIB}=\frac{AB}{BI}=\frac{1}{\sqrt{3}}\Rightarrow \widehat{AIB}=30°.$

Vậy góc giữa hai mặt phẳng (ACD) và (BCD) là $\widehat{AIB}=30°$