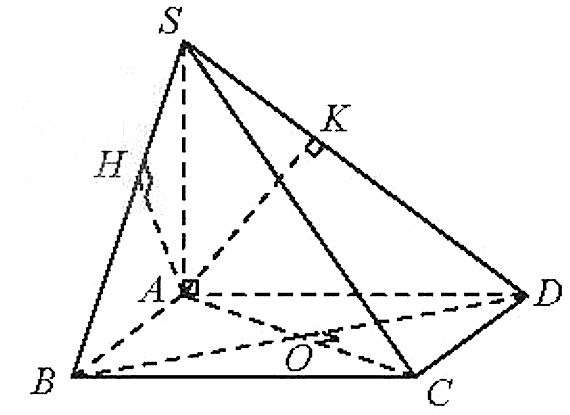
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi H và K lần lượt là hình chiếu của A trên SB và SD. Chứng minh rằng:

a) (SBC) ^ (SAB);

b) (SCD) ^ (SAD);

c) (SBD) ^ (SAC);

d) (SAC) ^ (AHK).

a) Theo giả thiết: 

$\left\{\begin{array}{l}\left(SAB\right)\perp \left(ABCD\right);\\ \left(SAD\right)\perp \left(ABCD\right);\\ \left(SAB\right)\cap \left(SAD\right)=SA.\end{array}\right.$

Suy ra SA ^ (ABCD).

Khi đó: $\left\{\begin{array}{l}BC\perp AB\left(ABCDlàhìnhvuông\right);\\ BC\perp SA(vìSA\perp \left(ABCD\right)).\end{array}\right.$

Þ BC ^ (SAB) Þ (SBC) ^ (SAB).

b) Theo giả thiết:

$\left\{\begin{array}{l}\left(SAB\right)\perp \left(ABCD\right);\\ \left(SAD\right)\perp \left(ABCD\right);\\ \left(SAB\right)\cap \left(SAD\right)=SA.\end{array}\right.$

Suy ra SA ^ (ABCD).

Khi đó: $\left\{\begin{array}{l}CD\perp AD\left(ABCDlàhìnhvuông\right);\\ CD\perp SA(vìSA\perp \left(ABCD\right)).\end{array}\right.$

Þ CD ^ (SAD) Þ (SCD) ^ (SAD).

c) Ta có: $\left\{\begin{array}{l}BD\perp AC\left(ABCDlàhìnhvuông\right);\\ BD\perp SA(vìSA\perp \left(ABCD\right)).\end{array}\right.$

Þ BD ^ (SAC) Þ (SBD) ^ (SAC).

d) Ta có:

(SAB) ^ (SBC) (Chứng minh trên);

(SAB) Ç (SBC) = SB;                           

Do đó AH ^ (SBC)

Mà AH ^ SB (giả thiết).

Nên AH ^ SC. (1)

Tương tự: AK ^ SC. (2)

Từ (1) và (2) suy ra: SC ^ (AHK).

Vậy (SAC) ^ (AHK).