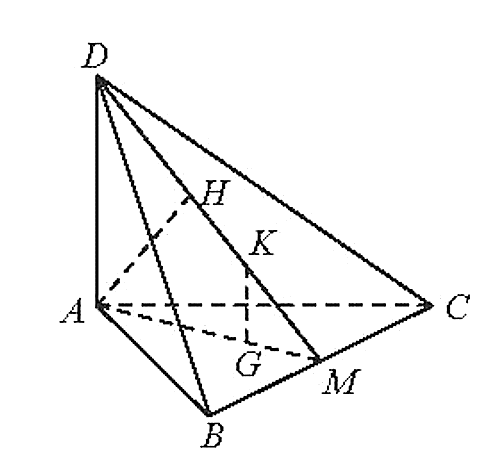
Cho tứ diện ABCD có DA ⊥ (ABC), ABC là tam giác cân tại A. Gọi M là trung điểm của BC.
Cho tứ diện ABCD có DA ⊥ (ABC), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ AH ⊥ MD tại H.
a) Chứng minh rằng AH ⊥ (BCD).
b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng GK ⊥ (ABC).