Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a căn 2
26
01/11/2024
Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a√2 . Biết rằng SA = SB = SC = SD, SO = 2a√2
a) Chứng minh rằng SO ⊥ (ABCD).
b) Tính độ dài đường cao xuất phát từ đỉnh A của tam giác SAC.
Trả lời
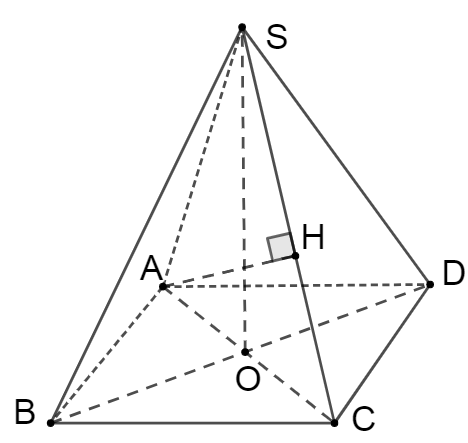
a) Từ giả thiết, dễ dàng nhận thấy ∆SAC và ∆SBD là các tam giác cân.
Ta có: {SO⊥ACSO⊥BD
Do đó SO ⊥ (ABCD)
b) Ta có: AC = 2a, OC = a, SC=√SO2+OC2=3a.
Vẽ đường cao AH của ∆SAC.
Ta có: AH=SO.ACSC=2a√2.2a3a=4a√23.
Vậy độ dài đường cao xuất phát từ đỉnh A của tam giác SAC bằng 4a√23 .

